第一回

化学とは何か

この講義について

理系学部にいて、将来化学に関連する研究をする可能性があり、化学の基礎を身につけたい人を対象とします。また、基本的な化学の語彙を身につけ、化学を物理の言葉で語れるようになることを目標としています。

具体的には、物理化学の一番基礎の部分を学びます。(教科書6章) 高校の化学は楽勝だった、という人には、ちょっと退屈かもしれません。

例年は、講義室でスライドを見せながら話し、時には板書をしていましたが、今年度はそのスタイルは難しいかもしれないと考え、4月1日にこのテキストを書きはじめました。使わなくても済むことを祈っていますが、3週間も先のことはまったくわかりません。

一般の教科書とちがい、講義で口頭で話すつもりだった内容を書き下していますので、不正確な情報や、個人的な感想や想像が含まれています。

また、教室で講義する場合には、毎回、演習問題を配布して講義の時間内に解いてもらい、理解度を確認しています。これが出席代わりになるのですが、今年はどうするかまだ決めていません。

成績評価は、例年は毎回の講義での演習が50%、最終試験が50%としていましたが、今年はこれもどうするか未定です。最終試験の比重を大きくする可能性があります。

この冊子にでてくる画像は断りがない場合はWikipediaから引用したものか、自作です。静止画に見えますが、クリック(タッチ)すると動画が再生されるものがあります。

化学とは

化学とは何でしょうか。高校生の感覚だと、物理の授業で物理の先生が教えてくれるのが物理、化学の授業で化学の先生が教えてくれるのが化学で、物理の先生が化学を教えたり、化学の先生が物理を教えたりすることはあまりないかもしれません。また、化学といえば周期表とか化学反応とか実験器具とか、そういった具体的なモノと結びつけて考えてしまうかもしれません。

物質を扱うのが化学、物体を扱うのが物理だ、という言い方をする人もいます。それも一理ありますが、実際には化学者も物体を扱いますし、物理学者も物質の根源を追究しています。

実際のところ、大学では物理、化学、生物、そして数学の区別はあまりはっきりしたものではありません。教科書売り場で、物理数学とか物理化学とか生物化学という題名の教科書が並んでいるのを目にしたことと思います。生物物理化学という、まるで理科総合科目のような題名の教科書すらあります。(でも、生物と物理と化学を網羅した教科書ではありません)

大学では、それぞれの学問が、より基礎にたちかえります。生物を学ぶには化学の知識が必要になりますし、化学を学ぶには物理の知識が必要です。そして、物理には数学が必要になります。この講義も、化学を物理のことばで学ぶことを目標にします。

物理は、「もののことわり」をひろく扱う学問なので、宇宙から素粒子まで、あらゆるものを扱います。その意味では、化学も物理に含まれます。では、なぜ物理の特定分野に、あえて化学という名前をつけるのでしょうか。なぜ、化学だけを専門とする化学者という人が、物理学者とは別に存在するのでしょうか。

それは、化学が扱う、「原子・分子のスケールの現象」が、ひときわ複雑で、そのスケールでしか起こらない現象があるからです。原子の種類が100以上もあること、それらを組みあわせてできる物質が無限にあり、しかもそれぞれの物質が個性的であるために、原子分子を扱う専門家が必要とされるのでしょう。

でも、多様で個性的な分子を収集し、分析するというだけだと、化学は(前世紀の)博物学のように聞こえますね。現代の化学は博物学ではありません。化学物質には多様な個性がありますが、その性質は、すべて物理の理論にもとづいて統一的に説明されます。これを担っているのが、「物理化学」という分野です。(私も物理化学者のはしくれです)

近代化学の黎明

今の化学(Chemistry)の基礎ができたのは1800年頃、今から200年ほど前にすぎません。化学の前身は、錬金術(Alchemy)や冶金学(やきんがく。鉱石から金属をとりだし、精製する技術)、そして薬学で、これらははるか古代エジプトから続いていました。

(http://embryology.med.unsw.edu.au/History/page2001.htm より引用)

それまでどうして錬金術は化学になれなかったのでしょうか。そして、どうしてその時期に化学が生まれたのでしょうか。時代背景を見ると、面白いことが見えてきます。

1800年よりもすこし前、1600年代に、デカルトやニュートンが近代の物理や数学を確立しました。デカルトのすぐ前の世代は、というとガリレオです。ガリレオは宗教家と対立し、「それでも地球は回っている」と言ったとか言わなかったとか言われていますが、デカルトは理性に基く近代哲学を提唱しました。彼は、世界を機械に譬え、世界は時計仕掛けのようであり、部品をひとつひとつ個別に研究した上で、最後に全体を大きな構図で見れば機械が理解できるように、世界も分かるだろう、という還元主義的な科学の手法を作った人といえます。片や同じ時代のニュートンは力学や微積分学の創始者として知られていますが、錬金術師でもありました。

この時代のできごとを調べてみると、科学の変化を予感させるさまざまな動きがあったことがわかります。ニュートンの晩年、18世紀はじめに水銀温度計が発明され、温度を「測る」ことができるようになりました。 18世紀末には地球の大きさを測定してメートルが規定されました。長さや温度や体積の尺度が、国を越えて共通になることで、科学の知識もまた国境を越えて共有できるようになりました。いわば情報革命が起こり、科学の進歩が加速したと考えられます。

化学にも大きな変革がやってきます。1800年に、Volta (イタリア)が電池を発明しました。すかさず同年には英国のカーライルとニコルソンが電気分解現象を発見しています。情報の流通が速くなっていた証左です。電磁気学や電流や電圧の概念が発見されるのはこれより20年もあとですから、化学者は電気とは何かを理解する前に、使い道を発見していたのです。

電気分解により、水を水素と酸素に分解できます。そして水素と酸素を反応させるとふたたび水に戻ります。電気分解によって、反応を逆行させ、物質を強制的に変化させることが可能になることで、化学の理解が一気に進展しました。化学の基本的な発見の多くは、19世紀の初頭に集中していることがわかります。

反応によって質量は変化しない。  (1789 Lavoisier 質量保存の法則)
反応する物質の質量比は簡単な整数比になる  (1803 Dalton 倍数比例の法則)
反応する気体の体積の比が非常に単純な整数比になる。  (1805 Gay-Lussac 気体反応の法則)
同温度、同圧力、同体積の気体に含まれる分子数は同一  (1811 Avogadroの法則)

気体

気体と工学

物質には気体、液体、固体の三態があります(注)。錬金術(冶金術、製薬も含む)は主に固体や液体を扱っていた印象がありますが、化学の発展をささえたのは気体の研究でした。(前節参照)それは、気体の性質が物質の種類によらず共通であるため、理論を作るのが容易だったためだと考えられます。

折しも1765年、英国のワットにより蒸気機関が発明されました。1769年にはフランスのキュニョが蒸気機関に車輪をつなげて、世界初の蒸気自動車を作り、世界初の自動車事故を起こしました。1783年にはモンゴルフィエ兄弟が熱気球により世界初の飛行をなしとげました。気体(蒸気)こそが、当時最先端の工学材料だったのです。

蒸気機関は19世紀に産業革命をもたらしました。それまでは、動力源といえば人力か、家畜の力か、水力風力ぐらいしかなかったのですが、蒸気機関により、はじめて人類は機械による力を手に入れます。蒸気機関の性能をいかに高めるかが、工学の重要な課題となります。そんな中、1823年にはカルノーが熱力学理論を打ち立て、熱機関の性能限界を予測しました。

熱力学は今でも最も重要で、最もひろくあてはめられる物理法則の一つです。現代の自動車のエンジンはもとより、ロケットエンジンや原子炉などの先端的な動力装置も、その性能の限界は熱力学によって規定され、それを越えることは不可能です。

ワットの蒸気機関。

*右: モンゴルフィエ兄弟の熱気球*

実験

ここで簡単な実験をしてみます。

準備するもの

風船
密封でき、中が見える箱
CO2ボンベ (自転車のパンク修理用や、水草育成用の小道具として手にはいります)

手順

風船を呼気でふくらませ、口を結んで閉じます。
風船を箱に入れ、箱の中をCO2で充満させてから蓋をします。

呼気の中にはほとんどCO2は含まれておらず、大部分が窒素と酸素です。また、風船はCO2をよく通しますが、窒素と酸素はほとんど透過しません。

質問

このまま放置すると、風船はどうなるか、このあとの話を聞きながら、予想して下さい。

1. しぼむ 2. そのまま 3. ふくらむ

容器のなかの風船。容器内はCO2で満たされているが、風船の内部は大気。

気体の基本法則

気体は、分子が乱雑に運動していて、しかも互いに離れている(凝集していない)状態をさします。とはいえ、分子は目に見えないので、この説明だけで気体のようすを想像するのは難しいかもしれません。そこで、計算機シミュレーションによるアニメーションを使いながら説明していきたいと思います。

気体の基本法則は、ボイルの法則、シャルルの法則、アボガドロの法則の3つです。

Avogadroの法則 : 同温度、同圧力において、同じ体積に含まれる分子の個数は等しい。
Boyleの法則 温度: 一定の時、気体は圧力に反比例して収縮する。
Charlesの法則 : 一定体積の気体の圧力は、温度に比例する。

こうやって並べてみると、うまい具合にABCの頭文字を持つことがわかります。中学校の理科で習うボイルとシャルルの法則には分子という言葉はでてきませんが、アボガドロの法則には分子がでてきます。

気体分子の運動。赤と青は、壁との衝突、分子同士の衝突を表す。

圧力

気体の基本法則のなかには、圧力や温度といった用語がでてきます。温度も圧力も、日常的な感覚として理解しているものと思いますが、気体分子の運動という観点ではどういうものか、アニメーションで見てみましょう。

分子が箱にとじこめられていると、分子は壁になんども激突し反射します。一度の衝突で壁は分子から撃力を受けます。この撃力の総和が、壁がうける圧力となります。

もうすこし正確に書きましょう。圧力とは、単位面積の壁が(気体分子から)受ける力のことで、単位はPa (パスカル=N/m²)です。あるいは単位面積あたり、単位時間あたり壁が(気体分子から)受ける撃力の和と言いかえることもできます。 (本当は、壁がなくても圧力を定義することはできますが、ここではわかりやすいように、固い壁を考えます)

分子が赤く光った瞬間に、分子から壁に撃力が伝わっています。

これを、ピッチャーが壁にボールを投げる状況で例えてみましょう。

壁をおさえる人には、投手の投げた球の撃力が伝わりますよね。

では、圧力を高めるにはどうすればいいでしょうか。圧力をN倍に高めるには、3つの方法があります。

1. 分子の速度をN倍にする

2. 分子の質量をN倍にする

3. 衝突頻度をN倍にする

温度

圧力と同じように、気体運動という観点から、温度をアニメーションで理解します。

分子の運動エネルギーは、絶対温度に比例します。これは何も気体に限ったことではありません。例えば、水を温める時に、コンロや電気ポットで、一定のペースで熱エネルギーを与えつづければ、温度もほぼ一定のペースで高くなっていくことは、経験的にわかると思います。

気体を分子の集まりだと考えると、個々の分子のもつ運動エネルギーは、E=mv²/2と表せます。(mは分子の質量、vは分子の速度) つまり、分子の速度が倍になると、運動エネルギーは4倍になり、温度も4倍になる、ということです。

低温の場合。例えばこちらを絶対温度300 Kとする。

高温の場合。分子速度が低温の倍なので、絶対温度は4倍、つまり1200 Kに相当する。

理想気体と現実の気体

ここまで、分子をただの球で表してきましたが、実際の分子はいろんな形があり、たとえば水分子はV字型、二酸化炭素はダンベル型です。また、分子の間に働く力も、分子によってかなり違います。ある条件のもとでは、こういった分子の個性が、気体の性質に反映される場合があります。

一方、気体の基本法則は、分子の種類によらない性質を記述しています。つまり、基本法則はある種の近似をおこなうことで、分子の個性を消しさり、異なる気体で共通に観察される性質だけを記述しているのです。

その近似は2つあります。

分子の間にはたらく斥力(反発力)を無視する。
分子の間にはたらく引力を無視する。

引力も斥力も無視したら、何も残らないじゃないか、と思うかもしれません。その通りです。両方を無視するということは、分子がほかの分子に一切力をおよぼさない、もっと単純に言えば分子がぶつかりもひきあいもせず、ただすりぬけるような状況を想定します。このような性質をもつ分子からなる気体のことを、理想気体と言います。

気体の密度が低い場合には、理想気体と現実の気体は、ほとんど区別がつきません。

理想気体。分子と分子は衝突せずにすりぬける。

現実の気体。分子と分子は時々衝突する。

ですから、密度が低い場合には、気体は多くの場合理想気体とみなして構いません。

しかし、密度が高くなると、近似が正確とは言えなくなります。

高密度の理想気体。分子と分子は衝突せずにすりぬける。

高密度の現実の気体。分子と分子は激しく衝突する。

このような近似の限界を念頭においた上で、気体の基本法則3つを、分子運動の観点からアニメーションで理解してみましょう。

シャルルの法則

「一定体積の気体の圧力は、温度に比例する。」

式で書くなら、p = C(V)•T (Cは比例定数)となります。

温度が4倍になると、圧力も4倍になる、という比例関係があると主張しています。実際にそうなるのか、分子運動を見てみましょう。

低温の場合。

高温の場合。分子速度は低温の2倍とした。

圧力の節で説明したように、圧力は速度と質量と衝突頻度に比例して増えます。また、温度の節で説明したように、分子速度が2倍になると、温度は4倍になります。

分子速度が2倍に増えると、分子が壁に衝突する速度が倍になるだけでなく、衝突頻度も倍になります。(壁から壁に移動する時間が半分になる)その結果、圧力も4倍になります。

ボイルの法則

「温度一定の時、気体は圧力に反比例して収縮する。」

式で書くなら、p•V=B(T) (Bは比例定数)となります。

体積を半分にすると、圧力が倍になる、と主張しています。これも実際にそうなるのか、分子運動を見てみましょう。

体積が半分になった時の、壁への撃力の変化を、上下の壁と側面の壁にわけて考えてみます。

側面の壁は、面積が半分になったために、面積あたりの衝突頻度は倍増する。
上下の壁の間を往復する分子は、壁の間隔が半分になったので、衝突頻度は倍増する。

これらの結果、圧力はどの面においても倍増します。

アボガドロの法則

「同温度、同圧力において、同じ体積に含まれる分子の個数は等しい。」

式で書くなら、V=A(p,T)•n (Aは比例定数)

アボガドロの法則は、分子に言及している点で、ほかの2つとは違った印象をうけます。 Boyleの法則もCharlesの法則も、明示的には書いてありませんが、異なる分子であっても同じ比例定数B,Cがそのまま使えます。 Avogadroの法則も場合も、異なる分子であっても同じ比例定数Aが使えるのですが、実際にそれを確かめてみます。

Avogadroの法則をそのまま検証すると難しくなるので、「同じ温度、同じ体積において、分子の個数が同じであれば、(分子の種類が違っていても)圧力は同じになる」ことを示してみましょう。

次の2つの動画は、どちらも同じ温度、体積、分子数ですが、分子の質量が違います。

分子量が小さい(軽い)分子の場合。

分子量が大きい(重い)分子の場合。(分子量は上の4倍)

温度が同じであれば、1分子の運動エネルギーは分子が重くても軽くても同じになります。

運動エネルギーはE=mv²/2ですから、分子質量mが4倍になれば、速度は半分になります。
分子の速度が半分になると、衝突頻度も半分になりますが、質量が4倍なので、撃力の総和としての圧力は1/2 x 1/2 x 4=1で変化しません。

三法則の統合

気体の基本法則三つを統合することで、pV=nRTという理想気体の状態方程式が得られます。これについては今日の演習課題に回しましょう。

圧力と温度は比例して、圧力と体積は反比例して…という風に覚えようとしても、なかなかすっと腑におちない人は、下のような立体グラフをイメージすると良いかもしれません。

理想気体の状態図 (http://hydrogen.physik.uni-wuppertal.de/hyperphysics/hyperphysics/hbase/kinetic/idegas.html より引用)

分圧の法則

「理想気体の混合物の圧力が各成分の分圧の和に等しい」

理想気体と、気体の分子描像をうけいれると、分圧の法則(ドルトンの法則)はとてもシンプルに理解できます。

今、青い分子だけが入った体積Vの箱と、赤い分子だけが入った体積Vの箱があり、どちらも温度はTとします。

青分子の個数とその圧力をn₁, p₁
赤分子の個数とその圧力をn₂, p₂

とすると、それぞれの箱で、p₁V=n₁RT, p₂V=n₂RTが成りたちます。同じ体積、同じ温度であれば、モル数の比が圧力の比になる、と読めます。

青分子の箱

赤分子の箱

さて、これらの分子を1つの箱(体積はV)に入れるとどうなるでしょうか。

理想気体を想定しているので、青分子と赤分子は互いに衝突せず、全くお互いに影響を与えません。すると、赤と青の分子が壁を叩いて壁に加える圧力は、それぞれの成分がもともと壁に加えていた圧力の和になります。

理想気体であれば、何種類の気体が含まれていたとしても、各成分ごとに圧力(分圧)を計算して、それらを足し合わせると全体の圧力になります。混合気体のなかに気体AとBがそれぞれモル分率0.6, 0.4の比率で含まれているなら、それぞれの成分の分圧は、全圧pに対して0.6p, 0.4pとなるわけです。

実験の続き

さきほど準備したケースの中の風船にふたたび注目して下さい。

(タイムラプスですが、遅くてうごきが見えにくいかもしれません。)

2、3時間待っていると、ケースの中の風船は自発的にふくらんできます。予想は当たったでしょうか?

風船が勝手にふくらむのはなかなか経験しないので直感に反するかもしれませんが、分圧の法則の時と同じような考えかたで理解できます。

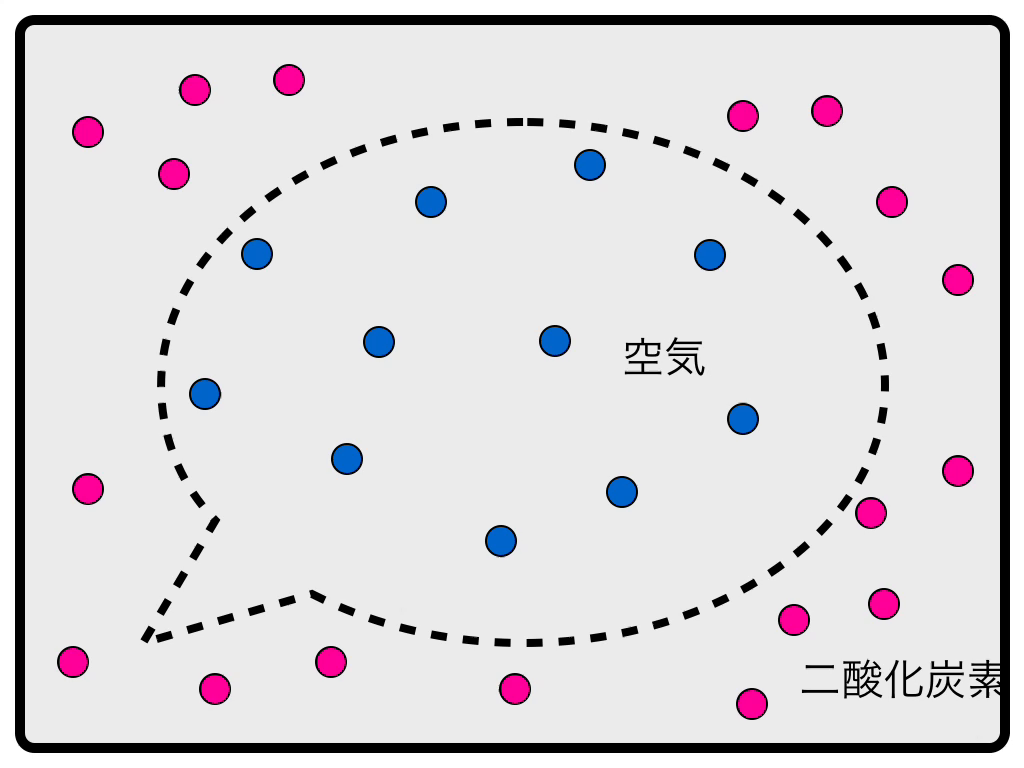
外側の四角がケース、内側の点線が風船だと思って下さい。風船のなかには通常の空気が、外には二酸化炭素が充満しています。これが最初の状態です。

風船のゴムは二酸化炭素をよく通しますが、それ以外の気体はほとんど通しません。内側の青の気体にとっては、風船の壁は越えられない壁ですが、外側の二酸化炭素はやすやすと壁を越えて風船の中に入ってきます。

すると、風船の内側には気体分子が最初の状態よりも多く入ることになり、風船がもし膨張できなければ、内部のほうが圧力が高くなります。(これを浸透圧と呼びます)

しかし、風船は柔軟な素材でできているので、内圧のほうが高くなったら、それを逃がすために膨張するのです。

実在気体

理想気体は、現実の気体に2つの近似(斥力を無視・引力を無視)を導入したものでした。そもそも、これらの力にはどういう意味があるのでしょうか。

分子間の斥力は、分子が一定距離よりも近付くのを妨げます。このため、体積が小さくなると、現実の気体分子は理想気体よりきゅうくつになり、分子が動ける体積が小さくなります。この効果をとりいれ、温度と圧力と体積の関係(状態方程式)をより現実に近付けるためには、体積に補正を加える必要があります。

分子間の引力は、どんな効果があるでしょうか。次に示すのは、分子間に斥力が働く場合と、斥力と引力の両方が働く場合の比較です。

斥力のみの場合。

斥力と引力の両方が働く場合。温度は上と同じ。

引力が働く場合には、集まって集合体を作るのがよくわかります。この状態が液体です。引力がない分子は液体になれません。温度が低い時には、分子の引力が熱運動にうちかって、互いにひきつけあうため、壁への撃力(圧力)は弱くなります。この効果をとりいれ、温度と圧力と体積の関係(状態方程式)をより現実に近付けるためには、圧力に補正を加える必要があります。

これらの効果をとりいれ、気体と液体の温度密度と圧力の関係を、低温低圧から高温高圧まで幅広く表現できるように定性的に補正した状態方程式がファンデルワールス状態方程式です。

ファンデルワールス状態方程式をさらに改良したRedlich-Kwongの状態方程式もあります。

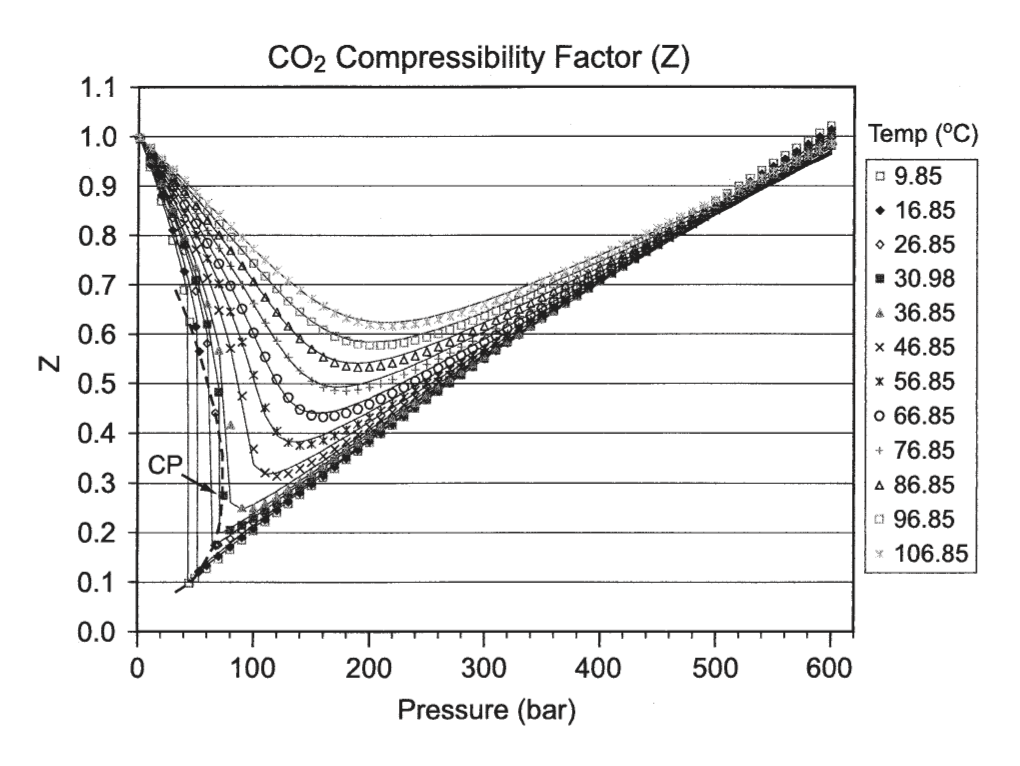
実在気体が、理想気体からどれぐらい違っているかを測る、便利な指標があります。z=pV/nRTで表されるzは圧縮因子と呼ばれ、理想気体なら1、理想的でない場合には1以外の値になります。これをプロットしたのが次の図です。

(Spycher and Pruess. Geochimica Et Cosmochimica Acta, 67(16), 17–17 (2003).より引用)

常温付近では、CO2はかなり理想気体から外れていることがわかります。これは、CO2の分子間力が強いことを意味します。実際、CO2はドライアイスになりますし、少し圧力を加えるだけで液体にすることも可能です。(実験で使ったCO2カートリッジの中にはCO2が液体状態で封じこめられています。)

圧縮因子が1より小さくなるということは、同じ温度圧力では体積が理想気体よりも小さくなることを意味します。低温低圧での収縮は、CO2の液化によるものです。

高圧では逆に圧縮因子が1よりも大きくなります。これは、分子同士の斥力により、分子が激しく衝突し、理想気体よりも圧力が高まることを意味します。

練習問題

練習問題は別ページに掲示します。

2020 基礎物質化学1

Edit