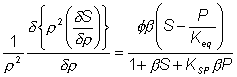|
|
Analysis of diffusional effects in porous supportsSo far, only external diffusional control of immobilised enzyme catalysed reactions has been described. This has been more due to the ease of the analysis rather than the scale of its application. Although it is undoubtedly extremely important, most immobilised enzyme catalysts are porous to some extent which necessitates the examination of the effect of internal diffusional resistance. Porous particles generally have very large surface areas of up to several hundred square metres per gram enabling very high immobilised enzyme loading. Where such biocatalysts operate under total external diffusional control (i.e., equation 3.27 holds) then the surface substrate concentration is effectively zero, no substrate is available for penetration into any pores and internal diffusion may be safely ignored as being of no importance. However, in all other cases it may well be relevant. This is because the pathways through which the substrate travel internally within the particles are generally much greater than those involved in external diffusional control (i.e., the pore length is several orders of magnitude greater than the depth of the surrounding stagnant layer, d). It should be noted that the effect of external diffusional limitations can be moderated, and sometimes removed completely, by changing the flow rate of the substrate solution over the biocatalytic surface, but such changes have no influence on the diffusion of the substrate within the protected environment of the interior of the particles. Diffusion of the substrate and product inside a porous biocatalyst occurs in parallel with the catalysed reaction. The more the enzyme catalysed reaction reduces the substrate concentration within the particles, the greater will be the substrate concentration gradient created between the internal microenvironment and the bulk of the solution. This, in turn, will increase the rate at which the substrate is delivered to the enzyme molecules towards the outside of the particles, increasing their effectiveness. The productivity of the reaction is, therefore, reduced considerably by the serious depletion of the substrate deep within the particle and the consequent high concentrations of product to be found there, possibly causing inhibition or reversing the reaction. To a certain extent, however, this is compensated by the increased flow of substrate to the outer portion of the immobilised enzyme particles due to the increased substrate concentration gradient. Analysis of the effect of internal diffusion is complicated by such factors as the shape of the particles, the distribution in size and shape of the pores, the total volume of the pores with respect to the particle volume (porosity, h), the depth to which the pores penetrate the particles (e.g., pellicular particles have only a thin layer of enzyme-containing pores at their surface), the tortuosity (t) of the route through the pores that the substrate encounters, the effective diffusivity of the reactants and products within the pores and the degree of uniformity of the enzyme's distribution within the particles (many immobilisation methods produce a higher volumetric concentration of enzyme towards the exterior of the immobilised enzyme particles, due to the rapid nature of the immobilisation reaction which immobilises the enzyme before it fully penetrates the pores). In order to examine the effect of these factors on a real system, it is useful to start with an analysis of the effect of internal diffusional resistance on the productivity of a 'model' porous biocatalytic particle. Beaded pellets are the most commonly encountered porous biocatalysts and may be considered as perfectly spherical for this purpose. The kinetics of other types of porous biocatalyst (e.g., flat membranous sheets, cylindrical pellets and fibres) may be analysed using a similar approach to that outlined here. A porous spherical particle of immobilised enzyme may be represented as shown in Figure 3.6. The simplified model used in this analysis also requires that
Under steady state conditions, the
net rate of diffusion of the substrate through a concentric slice of width
dr into a 'model' spherical immobilised enzyme particle at the radial
position r from its centre must equal the rate of reaction of the substrate
within that slice. The rate of substrate diffusion into the slice from the
outside equals the flux ( Simplifying and using the identity between
(
This may be further simplified by substitution with the dimensionless units; r for r/R, S for [Sr]/[SR], and b for [SR]/Km. The relative effects of internal diffusion and
the kinetic rate of reaction can be described by use of a substrate modulus for
internal diffusion (f) which is conceptually similar to m for
external diffusion. f, however is defined differently for each type of
porous biocatalyst (e.g., porous spheres, flat porous membranes, pellicular
particles). Substituting q for
( Therefore, as the slice width dr tends to zero An alternative definition of f (f#) which is linear with respect to the characteristic length of the system (in this case this is the ratio of the volume to surface area (R/3)) is sometimes used, where:
and, therefore, the two moduli are related by the expression:
This definition corresponds closer to that of m, the substrate modulus for external diffusion, in that it is linear with respect to length. Thus, increases in the radius of porous particles are shown to be an additional factor which may cause diffusional control in an immobilised enzyme catalysed reaction. The equation 3.50 cannot be solved analytically but may be solved by numerical methods using the boundary conditions that S and r are unity at the exterior surface of the particle, and r and dS/dr are zero at the centre of the particle. This latter condition is necessary for reasons of symmetry through the centre of the particle. The solution is achieved by an iterative choice of the substrate concentration at the centre of the particle and using the relationship 3.49 to describe the changes in the substrate concentration, in small steps, from the centre outwards to the surface of the particle until the first boundary condition is met to within the accuracy required. The resultant concentration profile, which can be rapidly obtained using a fairly simple microcomputer, enables the overall rate and effectiveness of reaction, catalysed by the particle, to be calculated. Clearly, only if the substrate concentration is unchanged throughout the particle will the effectiveness of the enzyme be unchanged relative to freely soluble enzyme (i.e., h = 1). This is unlikely to be approached except in the case of very low enzyme loading or very small particles. The substrate modulus (f) indicates the importance of these factors, being proportional to the enzyme loading and the square of the particle diameter and inversely proportional to the diffusion coefficient. In this example, it is also inversely proportional to the bulk substrate concentration as this governs the extreme value obtainable by the concentration gradient.
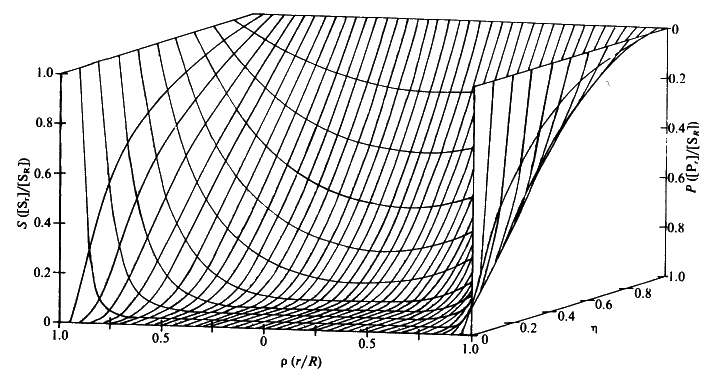
Figure 3.23. Substrate concentration profiles across spherical porous biocatalytic particles. The axes depict the substrate concentration relative to the external substrate concentration (S, which represents [Sr]/[SR]), the dimensionless radial position (r, representing r/R) and the effectiveness factor (h). The profiles were derived by changing the substrate modulus (f) while keeping b ([SR]/Km) constant (and equal to 0.1). Product concentration profiles are also shown; calculated assuming zero bulk product concentration and that the diffusion coefficients of substrate and product are equal.
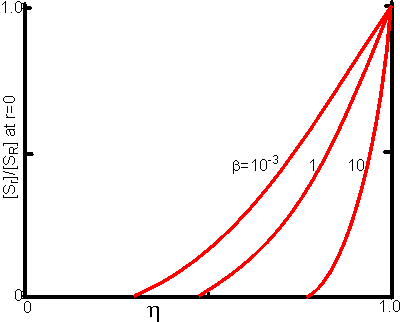
Figure 3.24. This shows the variation of the substrate concentration in the centre of immobilised enzyme particles with the effectiveness factor (h). Values for b (representing [SR]/Km) of 10, 1 and 10−3 are illustrated.
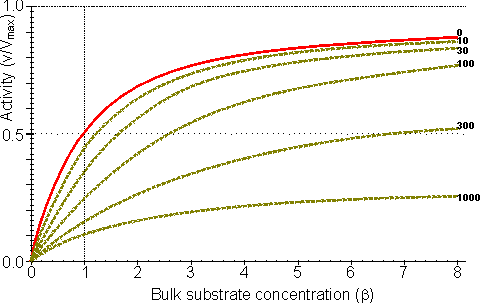
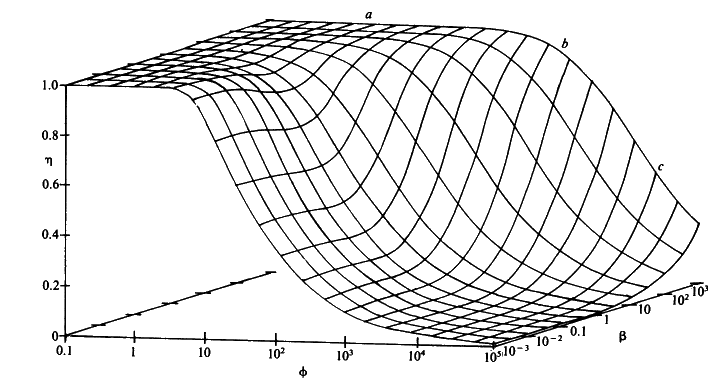
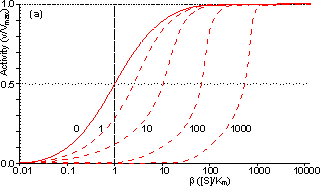
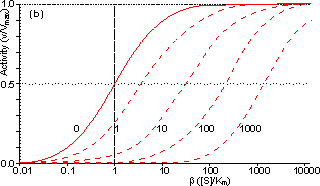
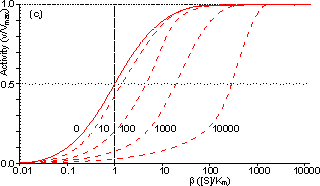
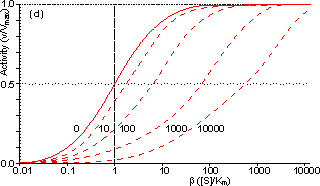
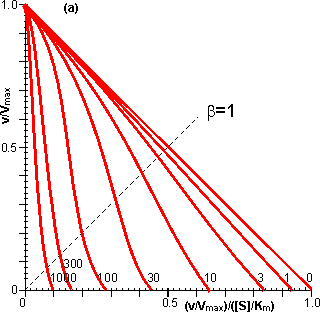
Figure 3.25. The variation in the rate of reaction catalysed by porous spherical particles containing immobilised enzyme with the dimensionless surface concentration of substrate, b (representing [SR]/Km). The top curve represents the case where there is no diffusional control (i.e., zero f') whereas the lower curves show the effect of progressively greater normalised substrate modulus for internal diffusion, f' (equalling 10, 30, 100, 300 and 1000). f' is the substrate modulus for internal diffusion (q) normalised with respect to the Km (i.e., f' = bf) in order to make it independent of the absolute value of the exterior substrate concentration. The shapes of the curves displayed should be compared with those encountered under conditions of external diffusional control (Figure 3.12). Particularly note the absence here of the significant linear portion at low b and high substrate modulus. The substrate concentration profiles across the particles at various effectiveness factors are shown in Figure 3.23. It can be seen that even at high h the substrate concentration drops significantly towards the centre of the particles and at low h this drop is so severe that the centres of the particles encounter very little substrate (Figure 3.24). This is particularly apparent at high b ([SR]/Km) as the reaction rate is close to Vmax and small changes in the substrate concentration do not significantly lower the effectiveness factor. The variation in the rate of reaction with substrate concentration and substrate modulus is shown in Figure 3.25. At low effectiveness factors, only the outer layer of the biocatalytic particle is utilised causing the particles to show an impressive apparent stability with time; relatively unused enzyme within the particle core only being brought into use as the surface immobilised enzyme inactivates due to denaturation. The variation of the effectiveness factor with the substrate modulus and the dimensionless substrate concentration is shown in Figure 3.26, which should be compared with the equivalent relationship for external diffusion shown in Figure 3.13. From this it can be seen that values of the substrate modulus below unity have little effect on the productivity of the immobilised enzyme particles, but higher values result in a considerable reduction in the effectiveness of the enzyme especially at low substrate concentrations.
Figure 3.26. The combined effect of the bulk substrate concentration b (representing [SR]/Km) and substrate modulus for internal diffusion (f) on the effectiveness factor (h) of porous spherical biocatalytic particles. The plateau (a) is an area of kinetic control, the graphical surface dropping through an area of intermediate control (b) to an area of diffusional control (c).
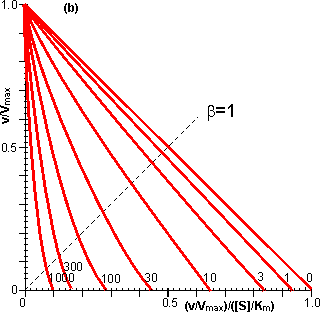
Figure 3.27. Semi-logarithmic plots for externally (a, b; m = 0, 0.1, 0.3, 1, 3 and 10) and internally (c, d; f' = bf = 0, 1, 3, 10, 30, 100, 300 and 1000) controlled reactions involving immobilised biocatalysts. (a) and (c) show non-reversible reactions whereas (b) and (d) have been calculated for the reversible reaction involving glucose isomerase (Keq = 1.14, bulk concentration of glucose (S) and fructose (P) being 51% and 42% (w/w), respectively, of the total carbohydrate).
Figure 3.28. Eadie-Hofstee plots for internally (f' = bf = 0, 1, 3, 10, 30, 100, 300 and 1000) controlled reactions involving immobilised biocatalysts. (a) non-reversible reaction, (b) reversible reaction involving glucose isomerase (Keq = 1.14, bulk concentration of glucose (S) and fructose (P) being 51% and 42%, respectively, of the total carbohydrate). These plots correspond to those shown in Figure 3.27 (c, d). Figure 3.18 (a, b) shows equivalent plots for Figure 3.27 (a, b). In real systems, the effectiveness factor is further reduced by steric effects which have been ignored in the above analysis. Where the substrate is large compared with the pore diameter, the effective diffusivity of the substrate within the pores will be significantly reduced, increasing f. This reduction is generally proportional to the tortuosity of the pore geometry (t) and inversely proportional to the particle porosity (h; see Figure 3.6 for definitions of t and h). The effective diffusion coefficient is additionally reduced as the ratio of the effective diameter of the substrate increases relative to the pore diameter, particularly where this ratio exceeds 0.02. This relationship usually causes a decrease in the effective diffusivity with the depth penetrated by the substrate. The active site of the enzyme may additionally be masked from binding the substrate by the difficulty with which the substrate can rotate within the confined space of the pores to give the correct effective conformation. The effectiveness factor may be increased by non-isothermal conditions where the reaction generates heat within the particles which is then unable to escape rapidly to the bulk phase. Non-isothermal operation is only rarely encountered as most enzyme catalysed reactions generate little heat and the catalytic particles are fairly small having large surface areas, through which the heat may escape, for their volume. Under circumstances where both external and
internal diffusion gradients are found, the flux of substrate through the
stagnant layer (
As the effective diffusion coefficient of the substrate within the particles (DS) is usually less than that in free solution, the substrate concentration gradient (d[S]/dr) within the particles must be greater than that occurring outside. Determination of the intrinsic kinetic constant (Km) is more complex in the case of internal than external diffusional control due to the added complexity concerning variation in the effective substrate diffusivity. It is best determined under conditions where q is less than unity, when little diffusional effect is apparent. Such conditions can be achieved by use of sufficiently small particles or low enzyme loading. Knowledge of the intrinsic Km value(s) and Vmax (obtained at high substrate concentrations, see Figure 3.27) allows the effective diffusion coefficients to be calculated. The effect of internal diffusional control on reversible or inhibited reactions is similar to that encountered under external diffusional control. It may be analysed as outlined earlier for uninhibited non-reversible reactions, but replacing the equation for the volumetric activity by one involving reversibility or inhibition. For example, in the case of the reversible glucose isomerase reaction, the Michaelis-Menten volumetric activity term in equation 3.46 may be replaced by that from equation 1.56. This gives the following relationship, after a similar derivation to that shown in equations 3.46 to 3.49, where P represents [Pr]/[SR], [Pr] represents the product concentration at radial position r and KSP replaces KmS/KmP. Under steady state conditions, the diffusion of substrate inwards, and product outwards are linked by the relationship where DP is the diffusion coefficient of the product.
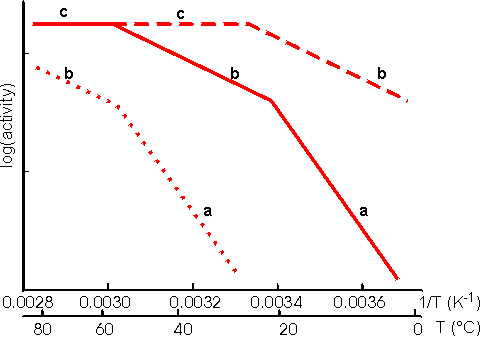
This value for P may be substituted into equation 3.54 and the resultant equation solved by an iterative numerical method as outlined previously. A comparison of the rates of reaction for non-reversible and reversible reactions under both internal and external diffusion control are shown in Figures 3.27 and 3.28. Figure 3.27 emphasises the fact that diffusional control of a reaction can be overcome at sufficiently high substrate concentrations whatever the type of control or substrate modulus (so long as the substrate remains soluble and no substrate inhibition occurs). The two types of diffusional control may be distinguished at the higher values of substrate modulus by the pronounced differences in the steepness of the sigmoidal curve in the intermediary range of reaction rates (e.g., between 10% and 90% of Vmax). This is because the rate of internally diffusion controlled reactions at low substrate concentrations are increased somewhat by the higher substrate flux through the outer layers of the porous biocatalysts. This effect can also be seen in the Eadie-Hofstee plots (Figure 3.28) at low rates of reaction. In practice, these graphs suffer from drawbacks if they are to be used to distinguish internal from external diffusional control. The semi-logarithmic plots need high substrate concentrations to be possible without these adversely affecting the reaction, whereas the Eadie-Hofstee plots are most prone to error within the area of interest. The difference between internal and external diffusional control is most noticeable in the variation in the rate of reaction with temperature. Reactions catalysed under conditions of external diffusional control obey equation 3.27. Their rates are independent of the activity of the enzyme and are, therefore, also almost independent of the temperature. Clearly, violent changes in temperature may affect the enzyme sufficiently that the rate of reaction is reduced below the rate at which the substrate can diffuse from the bulk of the solution, but then the reaction is no longer diffusionally controlled. Reactions catalysed under conditions of internal diffusional control do not obey equation 3.27. Increasing temperatures increase the rate at which the immobilised enzymes catalyse the reaction. This increases the substrate concentration gradient causing an increase in the flux of the substrate through the outer layer of the biocatalytic particles. Effectively, this halves the standard free energy of activation for the reaction relative to that catalysed by the free enzyme in solution. It should be noted that any such reduction in activation energy will reduce the effect of increased temperature on the reaction rates of immobilised enzymes. The relationship between the rate of reaction and temperature is shown schematically in Figure 3.29.
Figure 3.29. Schematic Arrhenius plots showing the progressive effect of diffusional limitations on the rate of reaction catalysed by porous particles containing immobilised enzyme. As the temperature increases the activity progresses through three phases (a), (b) and (c), in that order. (a) represents enzyme kinetic control of the reaction. The rate of reaction is sufficiently slow that no diffusional limitations are noticeable. The standard free energy of activation may be obtained from the gradient of this line. (b) represents control of the reaction rate by the internal diffusion of the substrate (i.e., the intrinsic rate of reaction has increased to greater than the rate at which substrate can diffuse into the particles). (c) represents control of the reaction rate by the diffusion of the substrate to the surface (i.e., the intrinsic rate of reaction has increased to greater than the rate at which substrate can diffuse through the stagnant layer surrounding the particles). No substrate is available for penetration into the pores. ----------- low enzyme loading, ——— intermediate enzyme loading,·········high enzyme loading. An Arrhenius plot using real data for an immobilised enzyme would show pronounced curvature between the three phases. The transition between the linear sections would not be readily discernible, over the range of temperatures normally encountered for the use of immobilised enzymes, unless the standard free energy of activation for the reaction was unusually high (e.g., above 75,000 J mole−1 for one of the transitions or above 100,000 J mole−1 for both transitions). Enzymic depolymerisation (including hydrolysis) of macromolecules may be affected by diffusional control. Large molecules only diffuse fairly slowly. After reaction, catalysed by the biocatalyst, the cleaved fragments normally retain their ability to act as substrates for the enzyme. They may diffuse away but are likely to be cleaved several times while in the vicinity of the immobilised enzyme. This causes a significant difference in the molecular weight profiles of the fragments produced by the use of free and immobilised enzymes. After a small degree of hydrolysis, most substrate molecules are cleaved by free soluble enzyme, whereas immobilised enzyme produces a small quantity of well-hydrolysed low molecular weight product with the majority of the substrate molecules unchanged. This process is exacerbated by the use of porous biocatalysts where there is some further restriction to the internal diffusion of large molecules. Use of immobilised enzyme is, therefore, indicated under circumstances where only a minimal proportion of partially hydrolysed product is required as it generally produces a mixture of almost fully hydrolysed moieties and unchanged polymer. The increase in the product concentration within the micro-environment may result in an increase in by-products caused by side reactions, especially where the reverse reaction catalysed by enzyme does not show complete specificity for the re-formation of the substrates. This is particularly apparent in the action of some carbohydrases. The increased microenvironmental product concentration may be utilised, however, where a reaction pathway is required. Co-immobilisation of the necessary enzymes for the pathway results in a rapid conversion through the pathway due to the localised high concentrations of the intermediates (Figure 30).
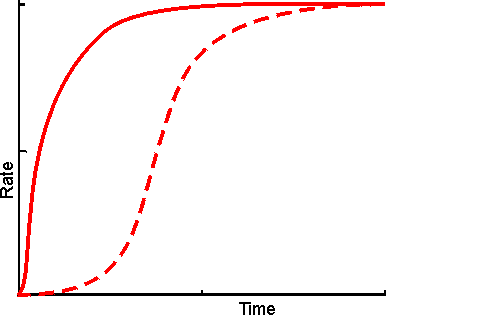
Figure 3.30. Schematic diagram showing the effect of co-immobilisation on the rate of production through a short reaction pathway. ---------- mixture of free enzymes, in solution; ——— co-immobilised enzymes showing a much reduced lag phase. The reduction in the apparent lag phase is most noticeable when there are more enzymes in the pathway. It is least pronounced where the flux through the pathway is controlled by the first step as the microenvironmental concentration of the initial substrate cannot be higher than its bulk concentration but those of all intermediates may be raised due to diffusional restriction on their rate of efflux. A logical extension of the use of immobilised multi-enzyme systems is the use of immobilised cell systems. These may be in a form which still allows respiration and reproduction or, in a restricted form, which cannot manage these functions but does retain catalytic activity. Sometimes they are treated with inhibitors or by physical means (e.g., heat) to ensure that only a sub-set of their natural enzymes remain active. Compared with immobilised multi-enzyme systems, immobilised cells are generally cheaper, easier to prepare with high activity, show little change in performance, on immobilisation, with respect to pH, ionic strength and temperature, and are generally preferred for use with metabolic pathways involving intracellular enzymes or dissociable cofactors or coenzymes. However they do suffer from a number of practical disadvantages. They are more prone to microbial contamination, less efficient with respect to substrate conversion to product, much more difficult to control and present diffusional problems due to their cell membranes.
This page was established in 2004 and last updated by Martin
Chaplin |
![r^2(d2[Sr]/dr^2) + 2r(d[Sr]/dr) = (Vmax/DS)r^2([Sr]/(Km + [Sr])](images/porous16.gif) (3.47)
(3.47) ![rho^2(d2S/dr^2) + 2r(dS/dr) = (VmaxR^2/DS[SR])r^2(beta S/(1 +bS)](images/porous7.gif)
![VmaxR^2/DS[SR]](images/porous17.gif) ) and combining the left
hand terms in
) and combining the left
hand terms in 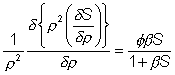
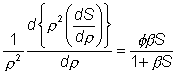
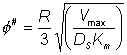 (3.51)
(3.51)