Amedeo Avogadro, a drawing by C. Sentier in 1856 — Amedeo Avogadro

Moles, molarity, and molality

Moles and mole fraction
Molality and molarity
% w/w , %w/v and % v/v

"...one mole (the molar or molecular weight of a substance expressed in grams)..."

W. Ostwald 1902

Moles and mole fraction

A mole (mol)^b is an amount (an official Système international d'unités, SI, unit having mass) of a substance and was originally defined as the amount that contains exactly the number of entities of that substance as there are ¹²C atoms in 12 grams (exactly) of ¹²C (this definition is now not used for the mole). The Dalton (Da) remains as defined as 1/12 of the mass of an unbound neutral atom of carbon-12; this is also known as an atomic mass unit, u. This number of entities in a mole is currently established as precisely 6.022 140 76 ˣ 10²³ ˣ mol⁻¹ [2395 ] and is known as the Avogadro number (see the portrait of Avogadro, above right). Thus, one mole of standard (VSMOW) water equals 18.015 265 g of water and contains 6.022 140 76 ˣ 10²³ (exactly) molecules of standard (VSMOW) water. The mole as an amount should not be confused with the exact but unitless number [4026 ]. The SI unit of concentration is mol ˣ m⁻³.

The mole fraction (sometimes called molar fraction) of water (x_w) is that (dimensionless) fraction of the molecules (and ions) present that are water molecules; that is,

x_w = moles water/(moles water + moles solute)

or for dilute solutions x_w = 55.5085/(55.5085 + 2 ˣ molality)

at 25 °C, for 1 : 1 electrolytes assuming that no water is bound to any solutes and also that all electrolytes dissociate completely into their stoichiometric number of ions [4100 ]. The molality of natural isotopic mixture (VSMOW) [IAPWS] water 25 °C is 55.5085 mol ˣ kg ^-1.

Thus, the mole fraction of 'free' water (x_w ) in an m (molal) salt solution is given by,

x_w = (m_w - m ˣ H_d)/(m_w - m ˣ H_d - m ˣ i_e)

where m_w is the molality of pure water, m is the molality of the salt, H_d is the hydrodesmic number (the dynamic average number of strongly bound water to the ions), and i_e is number of particles given by the extent of dissociation and ion pair formation [3505 ].

The mole fraction of a solute is the fraction of all the molecules (and ions) present that consist of that solute (that is, x_S= moles solute/(moles water + moles solute + moles other materials). At low solute concentrations, x_S may be approximated by

x_S = moles solute/moles water = molality ˣ molar mass of water = m_S ˣ M_H2O

where m_S is the molality, see below, and M_H2O is the molar mass of water = 0.018015265 kg ˣ mol⁻¹. This can be restated as

m_s = n_s /(n_H2O ˣ M_H2O)

where n_s and n_H2O are the numbers of moles of salt and water in the solution.

Note that 'moles' here refer to independent species such as molecules or ions. Care should be taken to correct concentration terms when the solution consists of a mixture of solutes where x_w = moles water/(moles water + moles solutes), or more precisely ^a

x_w = moles 'free' water/(moles 'free' water + moles solutes)

When considering colligative properties, these water molecules must be 'free' (see elsewhere), (that is, x_w = moles 'free' water/(moles 'free' water + moles solute). In contrast to the molality, bound water makes no difference to the numerical value of the molarity.

Molarity and molality.

These are different measures of solution concentrations and care should be taken to differentiate these terms.

Molality (m, with a lowercase, 'm'; molal concentration, be careful not to confuse it with 'm' for mass) is defined as the number of gram-moles dissolved per kilogram solvent; e.g., mol ˣ (kg water)⁻¹.

Molarity (M, with an uppercase, 'M'; molar concentration) is defined as the number of gram-moles dissolved per liter of solution; mol ˣ L⁻¹.

Conversion of molarity to molality and vice versa is often incorrectly described. The formulas are

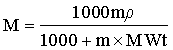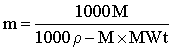
molarity=1000x molalityxdensity/(1000+molality x relative molecular mass) and molality=1000x molarity/(1000xdensity-molarity x relative molecular mass)

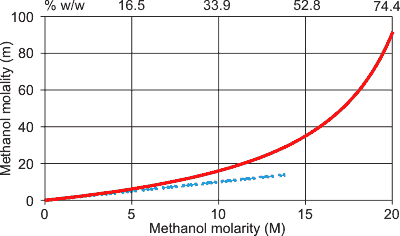
Molality compared with molarity, from [70]

where ρ is the experimentally determined density in g ˣ mL⁻¹ and MWt is the relative molecular mass of the solute. Allowance must be made for other solutes (and co-ions) present. Also, these equations do not allow for corrections due to any water bound to the solutes.

Opposite (shown red for methanol) are the very different values equivalent concentrations may have when expressed as molality or molarity. The lower blue dashed line indicates the relationship as the concentrations tend to zero and showing that there is little difference between molarity and molality at dilute concentrations. Molality is always numerically greater than the molarity. Note that % w/w (see below) on the top scale varies non-linearly with both molarity and molality.

Molarity versus molality for CsCl and LiCl

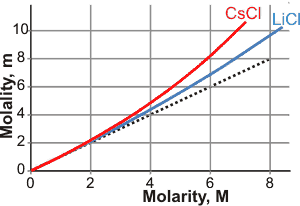
The figure on the left shows the molarity/molality relationship for CsCl and LiCl. Mistakenly using molarity in place of molality or vice versa, can lead to errors of about 2-4% for one molar solutions, 4-9% for two molar solutions and 10-30% for five molar solutions. At lower concentrations, such errors are primarily due to changes in the volume of the solution with temperature. The dependence of the molarity on temperature can be compensated by allowing for its thermal expansion. For small changes in temperature

Molarity at T = Molarity at T₀/(1 + α ˣ ΔT)

Where α is the thermal expansion coefficient (~0.000 25 K⁻¹ for dilute solutions) and ΔT is the temperature difference from the start temperature (T₀)

Molarity is most often used as it is easy to measure out volumes. However, such solutions are often less accurately prepared and dispensed due to the difficulties in attaining accurate volumes and the changes in volume that occur with temperature and pressure variation. Solutions with known molalities, prepared by weighing, are generally more precisely and accurately known and do not change concentration with temperature, pressure, or the addition of other solutes, so long as these solutes do not bind any of the 'free' (bulk) water present. Often, molarity is used for chemical reactions where the number of moles of reagent present is simply calculated (moles = molarity ˣ volume in liters). In contrast, molality should be used when physical or thermodynamic determinations are made, such as the determination of the colligative properties. Where there is a choice in the solvent (e.g., aqueous alcohol solutions), it is preferable to use the mole fraction rather than molality.

The SI unit of concentration is mol ˣ m⁻³ with molarity (M) and molality (m) being recommended for discontinuance by SI. It is expected that molal be replaced by mol ˣ kg⁻¹ and the rarely used term molality be discontinued as it may be confused with the more commonly used term molarity. However, these recommendations have not yet been generally accepted.

Osmolality is a variation of molality that only considers those solutes that contribute to a solution's osmotic pressure. It is measured in osmoles of the solute per kilogram of water. This unit can be determined simply from the depression of the freezing point of the solution. The term 'osmolarity' (although still in use in many textbooks) has been officially replaced by the term 'osmotic concentration' and is the product of the osmolality and the mass density of water.

The term 'Normality' (N) is sometimes encountered. It is analogous to molarity but refers to the charge equivalents rather than mole equivalents; thus, 0.1 M Ca²⁺ is the same as 0.2 N Ca²⁺.

Weight per weight, weight per volume, and volume per volume

There are other concentration units (often confused), such as % w/w (wt %, % by weight, % weight fraction, g dissolved in 100 g solution) % w/v (g dissolved in 100 mL solution), v/v (volume fraction), ppm (parts per million, mg/L), parts per thousand (‰, per mil, ppt), and ppb (parts per billion). The v/v is defined using the volume of a liquid component divided by the sum of the volumes of all the liquid components in the mixture when they are measured separately (IUPAC Gold Book). For example, 40 mL of ethanol + 60 mL of water is 0.4 v/v and a 40 % by volume solution but does not equal 100 mL of solution due to the reduction in volume on mixing. As it may be ambiguous (see below), it should be avoided wherever possible unless the molecular species present are not established. Note that mixing x mL of liquid material A with y mL of liquid material B rarely makes x + y mL of mixture unless they are immiscible. Also, note that ethanol's v/v (or % by volume) solutions are not the same as ABV (Alcohol By Volume) as used in the drinks industry. Unfortunately, this possible confusion has propagated on the web and is yet another reason for avoiding these units. For example, one may (correctly) make a 40% A by volume solution (40% v/v) by mixing 40 mL liquid A plus 60 mL water. Later this mixture may be made up to 100 mL by adding more water (i.e., the 100 mL mixture now contains more than 60 mL water). Another person sees that this 100 mL contains 40 mL of A and (mistakenly) calls it 40% A by volume (40% v/v).

The terms ppm and ppb can be used for highly dilute solutions or for impurities in materials, and they should be used together with w/w or w/v, as appropriate.

The volumes are generally not additive by-volume dilutions of liquids should never be made (i.e., the final volume is not the sum of the two volumes added). By-volume dilutions of by-weight concentrated solutions should never be made as the final concentrations may only be determined using knowledge of the densities of the solutions concerned, and the volumes are generally not additive.

[Back to Top ]

Footnotes

^a In many older textbooks, another (equivalent) way of treating moles 'free' water is as λ_w times x_w (λ_w.x_w) where λ_w is the activity coefficient of water and x_w is the calculated total mole fraction of water (i.e., 'free' water + 'bound' water). The activity coefficient (λ_w ) is just another way of specifying the 'free' fraction of water. [Back]

^b The SI definition of the mole is: 'The mole, symbol mol, is the SI unit of amount of substance of a specified elementary entity, which may be an atom, molecule, ion, electron, any other particle or a specified group of such particles; its magnitude is set by fixing the numerical value of the Avogadro constant to be exactly 6.022 140 76 ˣ 10²³ when it is expressed in the SI unit mol⁻¹ [2395] (exactly). [Back]