Quick links ...................................... Water molecule hydrogen-bonding Phase diagram Water spectrum Dissociation Anomalies Water properties ...................................... Water clusters Protein hydration Hydrocolloids Ions ...................................... Table of Contents Site map

Anomalous properties of water

Many of the properties of water are quite different from those expected from those of other liquids.

 

Unexpected properties of water

The range of anomalous properties of water

The rationale for the low-temperature anomalies of liquid water
Water phase anomalies
Water density anomalies
Water material anomalies
Water thermodynamic anomalies
Water physical anomalies

'Life on Earth as we know it would not exist if water was a regular liquid'

Kananenka and Skinner, 2020 [4035]

The range of anomalous properties of water

Water is in a class by itself with exceptional properties when compared with other materials. The anomalous properties of water are those where the behavior of liquid water is entirely different from what is found with other liquids [1414].^a The counterintuitive anomalies of water mostly arise from the properties of its hydrogen bonds, that also produce and control the local tetrahedral arrangement of the water molecules. The strength and directionality of the hydrogen bonds control liquid water’s thermodynamic and dynamic behavior. If hydrogen bonding did not exist, water would behave non-anomalously as expected from similar molecules. No other material is commonly found as solid (ice), liquid (water), or gas (steam).^d Frozen water (ice) also shows anomalies when compared with other solids. Although it is an apparently simple and small molecule (H₂O), it has a highly complex and anomalous character due to its inter-molecular hydrogen bonding (see [1530] for example). As a gas, water is one of the lightest known. As a liquid, it is much denser than expected although possessing a high void space. As a solid, it is much lighter than expected when compared with its liquid form. It can be extremely slippery and extremely sticky at the same time,^e and this 'stick/slip' behavior is how we recognize the feel of water [2411]. Water is the most cohesive molecular material in the Universe [3853]. Water is highly polar and very responsive to electric fields, including those produced by itself. Many other water anomalies may remain to be discovered, such as the possible link of water to room temperature superconductivity [2124]. ^h An interesting history of the study of the anomalies of water has been published [1542]. Explanations for the water anomalies should be broad enough to cover all the anomalies, with explanations suitable to only a sub-class of anomalies (and not suitable for others) being of interest but little utility.

 

As liquid water is so commonplace in our everyday lives, it is often regarded as a ‘typical’ liquid. In reality, water is most atypical as a liquid, behaving like an entirely different material at low temperatures to when it is hot, with a division temperature of about 50 °C. It has often been stated (for example, [127]) that life depends on these anomalous properties of water. The anomalous macroscopic properties of water are derived from its microscopic structuring and reflect the balance between low-density and high-density structures [3627].

 

The high cohesion between molecules gives it a high freezing and melting point, such that we and our planet are bathed in liquid water. The large heat capacity, high thermal conductivity, and high water content in organisms contribute to thermal regulation and prevent local temperature fluctuations, thus allowing us to control our body temperature more  efficiently. The high latent heat of evaporation gives resistance to dehydration and considerable evaporative cooling. It has unique hydration properties towards important biological macromolecules (particularly proteins and nucleic acids) that determine their three-dimensional structures, and their biological functions in solution. This hydration forms gels that can reversibly undergo the gel-sol phase transitions that underlie many cellular mechanisms [351]. Water ionizes and allows easy proton exchange between molecules, contributing to the richness of the ionic interactions in biology. It picks up positive charge when brushing against all materials tested except for air, where it picks up a negative charge [2703]. Also, it is an excellent solvent due to its polarity, high relative permittivity (dielectric constant), and small size, particularly for polar and ionic compounds and salts.

 

Tetrahedrally-linked hydrogen-bonded clusters are more prevalent at lower temperatures. The presence of a fifth water molecule close to these tetrahedra reduces at lower temperatures, see right [4195]. Both the average O···O distances within the tetrahedral clusters and the average O···O distances from the tetrahedral cluster water molecules to the next furthest (fifth) water molecules show different behavior at low and higher temperatures (shown in different colors, and more obvious with the furthest water molecules).

 

At 4 °C, water expands on heating or cooling. This density maximum together with the low ice density results in (i) the necessity that all of a body of freshwater (not just its surface) is close to 4 °C before any freezing can occur, (ii) the freezing of rivers, lakes, and oceans is from the top down, so permitting the survival of the bottom ecology, insulating the water from further freezing, reflecting sunlight back into space, and allowing rapid thawing, and (iii) density-driven thermal convection causing seasonal mixing in deeper temperate waters carrying life-providing oxygen into the depths. The large heat capacity of the oceans and seas allows them to act as heat reservoirs such that sea temperatures vary only a third as much as land temperatures, and so moderate our planet's climate (for example, the Gulf stream carries tropical warmth to northwestern Europe). The compressibility of water reduces the sea level by about 40 m giving us 5% more land [65].  Water's high surface tension and its expansion on freezing encourage rocks' erosion to provide soil for our agriculture.

 

Notable amongst the anomalies of water is the opposite properties of hot and cold water, ^b with the anomalous behavior more accentuated at low temperatures where the properties of supercooled water often diverge from those of hexagonal ice. In particular, several properties of water change at about 50 °C [2755], just above the body temperature of mammals and about which many proteins denature. As (supercooled) cold liquid water is heated, individual molecules shrink, bulk water shrinks and becomes less easy to compress, ^j its refractive index increases, the speed of sound within it increases, gases become less soluble, it is easier to heat, and it conducts heat better. In contrast, as hot liquid water is heated it expands, it becomes easier to compress, its' refractive index reduces, the speed of sound within it decreases, gases become more soluble, it is harder to heat, and it is a poorer conductor of heat. With increasing pressure, individual molecules expand, cold water molecules move faster, but hot water molecules move slower. Hot water freezes faster than cold water, and ice melts when compressed, except at high pressures, when liquid water freezes when compressed.

 

Fluctuations in liquid water^h

<(ΔV)²>_TPN = T ˣ κ_T ˣ V ˣ k_B

 

<(ΔV)(ΔS)>_TPN = T ˣ α_P ˣ V ˣ k_B   

 

<(ΔS)²>_TPN = T ˣ C_P ˣ k_B  

 

increase upon cooling below about +43 °C, and down to the homogeneous ice nucleation temperature (≈ -45 °C), instead of decreasing as expected. In liquids, it is generally expected that the entropy and volume are positively correlated, with their fluctuations decreasing as the temperature decreases. In water, however, the entropy and volume are negatively correlated with a volume increase, bringing an entropy decrease.

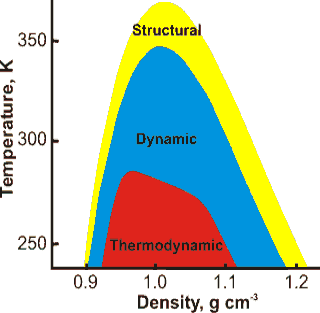
The anomalies of water appear as a hierarchy of effects with different bounds [169]. These are shown indicatively opposite as derived from modeling, not experimental data. The ‘Structural’ bounds indicate where water is more disordered when compressed, the ‘Dynamic’ bounds indicate where diffusion increases with density, and the ‘Thermodynamic’ bounds show where there is a temperature of maximum density. ^g As density always increases with increasing pressure, a similar relationship holds with pressure along the horizontal axis. Phase diagrams of other tetrahedrally structured liquids (e.g., Si, SiO₂) also show the nesting of anomalous regions [2285]. The relationships between different anomalies have been derived from the underlying thermodynamic relationships [3733].

 

The onset of interpenetration causes other anomalies of water at about 200 MPa, such as the high-pressure C_P anomaly [2929], the density-distance paradox, and the fast-sound anomaly.

 

[Back to Top ]

The rationale for the low-temperature anomalies of liquid water

Four different scenarios have been suggested:

 

(1a) The stability limit conjecture. There is a limit (a singularity) to the mechanical stability of water at -45°C, 0.1 MPa [1886, 2995]. This was suggested to be associated with the cooperative formation of an open hydrogen-bonded network.

 

(1b) A singularity-free scenario. It was suggested that the most straightforward interpretation of the behavior of supercooled water consistent with experimental observations is free of singularities [11, 2996]. This is consistent with supercooled water approaching the structure of a fully bonded random or non-random (e.g., ES) tetrahedral network on cooling. This may or may not be linked to a critical point at higher or negative pressure.

 

(2a) A liquid-liquid critical point (LLCP) [3753, 3954]. Increasingly, scientists attribute the low-temperature anomalous nature of water to the presence of a metastable second critical point at about -80°C (under positive pressure, about 180 MPa), when high-density liquid water and low-density liquid water no longer coexist within the same phase [2930, 3134], but split into different phases, separated by a first-order phase transition (i.e., the liquid-liquid phase transition, LLPT). Using TIP4P/2005 and TIP4P/Ic modeling, has also indicated that a metastable liquid-liquid critical point occurs under deeply supercooled conditions and that a low-density liquid may nucleate from within a high-density liquid and vice versa [4010]. Progress of research into liquid-liquid transitions in various single component substances has been reviewed together with a detailed discussion of how the existence of two or more liquids (glasses) for a single-component substance can be physically rationalized [4152]. There is still some dispute over the presence of a second critical-point, particularly over whether it should really be called a critical point considering the phases are metastable [4433].

 

(2b) A critical point-free scenario. Rather than a critical point, the "fragile-to-strong" transition for supercooled water is interpreted as the reason for the anomalies in supercooled water [312l].

 

It has been established that scenario 1b is inconsistent with the evidence and that a second critical point exists [2144 e,f, 2602, 2930, 3202, 3134, 3420, 3851, 3954]. The existing data supporting the other scenarios are all consistent with scenario 2a. Water's anomalies do not require scenario 2a as an explanation (as agreed by [4122] and [4142] after an extensive review of the relevant literature). However, it does seem likely [2947] that there is such a phenomenon and that it could enable the attributed effects [3954], depending on its precise position in the phase space. The liquid-liquid critical point scenario does not contain any information concerning the structure of the two phases involved. In this respect, it is a somewhat unproductive hypothesis as a sole explanation of these anomalies (as the attribution mixes cause with effect, as agreed by others [1859]. The anomalies may simply be caused by the presence of the two phases in proportions determined by their temperature and pressure [4094]. However, when linked to an equation of state (EOS) that can predict the (low temperature) spinodal ^j in the presence of the second critical point, it may be used to explain several of water's anomalies [3954]. Therefore, liquid water may be considered as a locally-inhomogeneous supercritical fluid that fluctuates between a low (mostly tetrahedral expanded) and a high-density (mostly collapsed) liquid states. The former is enthalpy-driven, and the latter is entropy-driven. A description of the structures is given elsewhere. In 2020, there were experimental observations of the liquid-liquid transition in bulk supercooled water under pressure, so reinforcing scenario 2b [4220].

[Back to Top ]

Water density anomalies

1. The density of ice increases on heating (up to 70 K). [Explanation]
2. Water shrinks on melting. [Explanation]
3. Pressure reduces ice's melting point. [Explanation]
4. Cold liquid water has a high density that increases on warming (up to 3.984 °C). [Explanation]
5. The surface of water is denser than the bulk. [Explanation]
6. Pressure reduces the temperature of maximum density. [Explanation]
7. There is a minimum in the density of supercooled water. [Explanation]
8. Water has a low coefficient of expansion (thermal expansivity). [Explanation]
9. Water's thermal expansivity reduces increasingly (becoming negative) at low temperatures. [Explanation]
10. Water's thermal expansivity increases with increased pressure. [Explanation]
11. The number of nearest neighbors increases on melting. [Explanation]
12. The number of nearest neighbors increases with temperature. [Explanation]
13. Water has unusually low compressibility. [Explanation]
14. The compressibility drops as the temperature increases up to 46.5 °C. [Explanation]
15. There is a maximum in the compressibility-temperature relationship. [Explanation]
16. The speed of sound increases with temperature up to 74 °C. [Explanation]
17. The speed of sound may show a minimum. [Explanation]
18. 'Fast sound' is found at high frequencies and shows a discontinuity at higher pressure. [Explanation]
19. The NMR spin-lattice relaxation time is very small at low temperatures. [Explanation]
20. The NMR shift increases to a maximum at low (supercooled) temperatures [Explanation]
21. The refractive index of water has a maximum value at just below 0 °C. [Explanation]
22. The change in volume as liquid changes to gas is very large. [Explanation]

[Back to Top ]   

Water material anomalies

1. No aqueous solution is ideal. [Explanation]
2. D₂O and T₂O differ significantly from H₂O in their physical properties. [Explanation]
3. Liquid H₂O and D₂O differ significantly in their phase behavior. [Explanation]
4. H₂O and D₂O ices differ significantly in their quantum behavior. [Explanation]
5. The mean kinetic energy of water's hydrogen atoms increases at low temperatures (disputed). [Explanation]
6. Solutes have varying effects on properties such as density and viscosity. [Explanation]
7. The solubilities of nonpolar gases in water decrease with temperature to a minimum and then rise. [Explanation]
8. The dielectric constant of water and ice are high. [Explanation]
9. The relative permittivity shows a temperature maximum. [Explanation]
10. The relative permittivity shows a 'kink' in its behavior with the temperature at 60 °C. [Explanation]
11. The imaginary part of the dielectric constant shows a minimum near 20 K. [Explanation]
12. Proton and hydroxide ion mobilities are anomalously fast in an electric field. [Explanation]
13. The electrical conductivity of water rises to a maximum at about 230 °C. [Explanation]
14. The electrical conductivity of water rises considerably with frequency. [Explanation]
15. Acidity constants of weak acids show temperature minima. [Explanation]
16. X-ray diffraction shows an unusually detailed structure. [Explanation]
17. Under high pressure water molecules move further away from each other with increasing pressure, a density-distance paradox. [Explanation]
18. Water adsorption may cause negative electrical resistance. [Explanation]

[Back to Top ]   

Water thermodynamic anomalies

1. The heat of fusion of water with temperature exhibits a maximum at -17 °C. [Explanation]
2. Water has over twice the specific heat capacity of ice or steam. [Explanation]
3. The specific heat capacity (C_P and C_V) is unusually high. [Explanation]
4. The specific heat capacity C_P has a minimum of 36 °C. [Explanation]
5. The specific heat capacity (C_P) has a maximum of about -45 °C. [Explanation]
6. The specific heat capacity (C_P) has a minimum with respect to pressure. [Explanation]
7. The heat capacity (C_V) has a maximum. [Explanation]
8. The high heat of vaporization. [Explanation]
9. The high heat of sublimation. [Explanation]
10. The high entropy of vaporization. [Explanation]
11. The thermal conductivity of water is high and rises to a maximum at about 130 °C. [Explanation]

[Back to Top ]   

Water physical anomalies

1. Water has unusually high viscosity. [Explanation]
2. Large viscosity and Prandtl number increase as the temperature is lowered. [Explanation]
3. Water's viscosity decreases with pressure below 33 °C. [Explanation]
4. Large diffusion decrease as the temperature is lowered. [Explanation]
5. At low temperatures, the self-diffusion of water increases as the density and pressure increase. [Explanation]
6. The thermal diffusivity rises to a maximum at about 0.8 GPa. [Explanation]
7. Water has unusually high surface tension. [Explanation]
8. Some salts give a surface tension-concentration minimum, the Jones-Ray effect. [Explanation]
9. Some salts prevent the coalescence of tiny bubbles. [Explanation]
10. The molar ionic volumes of salts show maxima with respect to temperature. [Explanation]

[Back to Top ]   

---

 

 

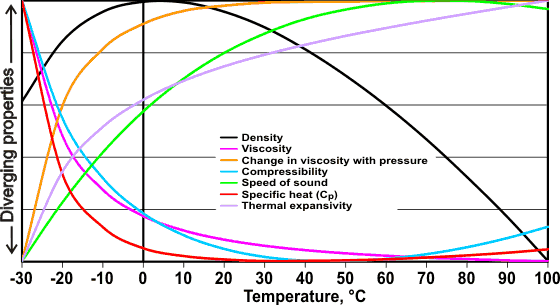
The figure left shows some of the anomalous properties of liquid water that are related to temperature. The graph uses data that have been scaled between their maximum and minimum values within this range (see original data). Note, in particular, the different behaviors at high and low temperatures that is in marked contrast to the behavior of simple liquids, whose thermodynamic properties vary in a monotonic manner with temperature.

 

In addition to these anomalous properties of water, other properties show unexpected relationships.

---

Footnotes

^a   Whether or not the properties of water are seen to be anomalous depends upon the materials used in the comparison and the interpretation of the term 'anomalous'. For example, it could well be argued that water possesses exactly those properties that one might deduce from its structure (see, [402]). The small number of other tetrahedrally interacting liquids (without any hydrogen bonds), such as liquid Si [1835], SiO₂, Ge, C, Sb, Bi, Ga, GeO₂, GaAs, InSb, CdTe, and BeF₂ have many similar 'anomalies' [1814, 4402], as do other materials (also without any hydrogen bonds) where mixed phases may arise, such as liquid Te [1538]. Comparisons between water, liquid sodium, liquid argon, and benzene appeared to Franks [112] to indicate several properties given above as not anomalous. However, these materials are perhaps not the most typical of liquids, and elsewhere Franks endorses water's anomalous nature. Also, other liquids (e.g., hydrazine, N₂H₄, has a melting point of 2 °C, and a boiling point of 114 °C) are multiply hydrogen-bonded but do not show similar anomalies. Stating that the properties of water are not 'anomalous' but are 'special' [3219] does not clarify the situation. This list gives the unusual properties generally understood to make liquid water (and ice) stand out from 'typical' liquids (or solids). See [242] for a review concentrating on the non-anomalous properties of water, that is, those that are the 'same' as for other liquids. At higher temperatures (>315 K) the thermodynamic properties of water may be considered close to 'normal' for a liquid [1638]. Note that properties that are compared at ambient pressure or along the vapor/liquid line may be seen as anomalous, whereas under isopycnic (isodensity) conditions no (anomalous) maximum or minimum values may be found (for example, no specific heat minimum, speed of sound maximum or compressibility minimum are found at constant water density of 1 g cm⁻³; see line on phase diagram).

 

It is generally agreed by water scientists today that water is the most anomalous substance [2653, 3354]. [Back]

 

^b    Some scientists attribute the low-temperature anomalous nature of water to the presence of a second critical point; an interesting if somewhat unproductive hypothesis as a sole explanation (as the attribution mixes cause with effect, as also latterly agreed by others [1859]). Water's anomalies do not require this as an explanation, although it does seem likely [2947]. [Back]

 

^c    The temperature range of 'hot' and 'cold' water varies in these examples; see the individual entries for details. [Back]

 

^d    The anomalies of water are divided into groups, but some anomalies may be included under more than one topic, and there may not be a universal agreement for the groupings shown. The 'number' of anomalies depends on which ones are chosen and whether related anomalies (such as the reciprocal variations including molar volume and density) are grouped together or as separate phenomena. [Back]

 

^e   This is easily shown with two wet panes of glass. If one wet pane is placed horizontally on top of the other, then the panes easily slip over each other horizontally (i.e., they are very slippery) while it being almost impossible to separate the sheets in the vertical direction (i.e., they are very sticky). This phenomenon does not occur with dry panes of glass. A further example of water's stickiness is its use in making sandcastles, whereas its slipperiness is well known on wet floors that are many orders of magnitude more slippery than when dry. Landslides may be triggered by heavy rain, causing slipping at the interfaces between soil particles. The slipperiness of water is used in joints between our bones, allowing their easy relative movements [3990]. The stickiness of water ice in the outer reaches of protoplanetary disks enhances the growth of water-containing rocky asteroids and planets as the particles stick together [2251]. This stickiness/slipperiness anomaly is even more extreme if ice cubes are considered. Keep them moving next to each other then they are very slippery; however, if they stop moving them, then they will stick together forever.

 

Eels are very slippery due to their water coating. This slipperiness can be neutralized by putting the eel on newspaper. [Back]

 

^f   The data from [169] is shifted 38 K upwards to give the correct temperature of maximum density under standard pressure. [Back]

 

^g  Sometimes, apparently unpredictable or unexpected properties of liquid water may be due to variations in the dissolved gas concentrations [1948], a factor that is difficult to control and easy to overlook. Atmospheric gases dissolve in water to form nanobubbles and microbubbles, some of which may expand and rise back to the surface. This process causes continuous but somewhat chaotic changes in the gaseous concentrations over significant periods (» 100 s) and consequently continuous changes in the hydrogen-bonded structuring within the water [1948]. Such artifacts are thought to be absent in the anomalous properties described above. [Back]

 

^h  Where <(ΔV)²>_TPN is the mean square fluctuations in volume (V) for constant temperature (T), pressure (P), and number of molecules (N), <(ΔV)(ΔS)>_TPN is the fluctuation correlation in volume, and entropy for constant temperature, pressure, and number of molecules, <(ΔS)²>_TPN is the mean square fluctuations in entropy for constant temperature, pressure, and number of molecules, κ_T is the isothermal compressibility, k_B is the Boltzmann constant, α_P is the thermal expansivity, and C_P is the heat capacities at constant pressure. [Back]

 

ⁱ  J. Canton, Experiments and observations on the compressibility of water and some other fluids, Phil. Trans. 54 (1764) 261-262. [Back]

 

^j   Spinodal. The limit of local thermodynamic stability (e.g., outside this limit, there is no stable or metastable continuation) with respect to small fluctuations is defined by the condition that the second derivative of Gibbs free energy (e.g., with respect to density) is zero. The locus of these (inflection) points is known as the 'spinodal' curve. Spinodal curves end in critical points. [Back]

 

 

Home | Site Index | Explanation of the anomalies | Water: Introduction | The icosahedral water clusters| LSBU | Top

 

This page was established in 2003 and last updated by Martin Chaplin on 19 November 2020

This work is licensed under a Creative Commons Attribution
-Noncommercial-No Derivative Works 2.0 UK: England & Wales License