
Low density icosahedral (H2O)280 cluster
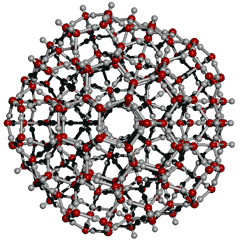
There has been growing support for liquid water containing hydrogen-bonded clusters related to icosahedral clustering.
Henry S. Frank and Wen-Yang Wen (1957)
![]() Overview of the structure of liquid water
Overview of the structure of liquid water
![]() Introduction to water clustering
Introduction to water clustering
![]() The icosahedral water cluster, (H2O)280
The icosahedral water cluster, (H2O)280
![]() Cluster equilibria
Cluster equilibria
![]() Radii
and occupancy of the shells of expanded clusters
Radii
and occupancy of the shells of expanded clusters
![]() Sphericalcoordinates of the icosahedral water clusters
Sphericalcoordinates of the icosahedral water clusters
![]() Super-clusters of water molecules
Super-clusters of water molecules
![]() The radial distribution function
The radial distribution function
![]() Other support from diffraction data
Other support from diffraction data
![]() How
can a liquid have a structure?
How
can a liquid have a structure?
![]() Does the radial distribution
peak at about 3.7
Å
exist?
Does the radial distribution
peak at about 3.7
Å
exist?
![]() Is there a fine structure
in the radial distribution function?
Is there a fine structure
in the radial distribution function?
![]() Are there interstitial
water molecules?
Are there interstitial
water molecules?
![]() Support from clathrate structures
Support from clathrate structures
![]() Evidence from amorphous ice and low-density water
Evidence from amorphous ice and low-density water
![]() Other evidence
Other evidence
![]() The fragile to strong transition
The fragile to strong transition
'any model that claims agreement with the observed diffraction pattern of liquid water should reproduce
not only the first peak but all other significant features of the radial distribution function as well'
Narten and Levy (1969) [767c]
First radial distances
Although the icosahedral cluster model can explain the anomalous properties of water, so can other models to varying extents. The most substantial direct evidence for this model is the agreement with the radial distribution functions. g The CS model was used to generate a radial distribution of the O···O distances. Figure 1 compares this radial distribution function with that from the X-ray data at 4 °C [9], which shows a great deal of fine structure. Although the peaks are in the same positions, they are less distinct in the X-ray data indicating the relative movements expected of a liquid and the relatively long time taken to achieve the spectrum. There are 14 peaks or troughs in the goo-r plot, plus a further 36 inflection points evident using the first derivative (peaks and troughs in the Δgoo/Δr plot). All 50 positions show correspondence between the X-ray data and the calculated function for CS, except between about 7.9 Å and 8.5 Å, where two peaks and troughs in the first derivative X-ray data only had corresponding inflection points in the first derivative CS model data. If we consider all 50 data, the standard deviation of the differences between the X-ray data and the CS model data is less than 1% (0.065 Å). This correspondence, between the model and the experiment, is qualitatively indicative of the presence of the described clusters (or significantly large fractions of the clusters or partial clusters). Also it agrees with the 2011 wide-angle X-ray diffraction measurements [1755] that were explained as a tetrahedral minority structuring within a more disorganized majority water structuring. There is also good correspondence with the O···O radial distribution functions derived from the neutron diffraction data, although this experimental data shows less fine structure [36].
The radial distribution function of the O-O distances
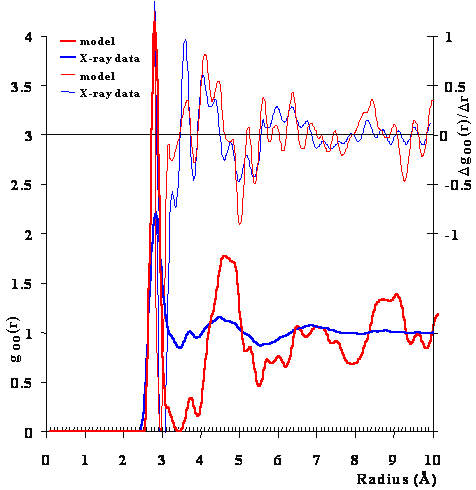
Figure 1. Comparison of the calculated oxygen radial distribution function from the model with the early but information-rich X-ray diffraction data of Narten [9] of near-surface water at 4 °C. There are 14 peaks or troughs plus a further 36 inflection points evident using the first derivative (above, diffraction data scaled ˣ 5). c
Peak/trough, Å |
Inflections, Å |
||||
|---|---|---|---|---|---|
Model |
X-ray |
Model |
X-ray |
||
2.81 3.44 3.73 3.91 4.52 5.52 7.00 7.90 8.72 8.88 9.08 9.43 9.63 9.85 |
2.83 3.46 3.72 3.91 4.49 5.55 6.86 7.83 8.79 9.03 9.18 9.42 9.62 9.84 |
2.69 2.90 3.16 3.26 3.63 3.81 4.09 4.28 4.46 4.73 4.82 5.01 5.24 5.39 5.61 5.76 5.95 6.11 |
6.36 6.65 6.86 7.06 7.12 7.30 7.47 7.64 7.91 8.00 8.44 8.59 8.65 8.83 9.00 9.27 9.52 9.72 |
2.65 2.99 3.25 3.34 3.60 3.80 4.05 4.24 4.36 4.60 4.76 4.99 5.19 5.36 5.60 5.71 5.95 6.15 |
6.35 6.59 6.75 6.99 7.15 7.35 7.56 7.65 7.89 8.07 8.31 8.52 8.70 8.90 9.10 9.30 9.51 9.72 |
X-ray diffraction data has confirmed the peak at about 3.4 Å and the double-peak feature at about 4.5 Å [1631, 1788a/c]. The peak at 3.4 Å is usually included with the 2.82 4 Å peak when the number of water molecules within the area of the first peak up to the first minimum is calculated, giving the often-quoted value of about five molecules of water around each water molecules [58]. The high peaks at high radius (8.72 Å, 9.08 Å and the rise approaching 10.5 Å) are in agreement with those found by wide-angle x-ray scattering and due to five-member pentamer rings [3625]. Also, other X-ray diffraction data on supercooled water has reinforced the above observations and supports the presence of clathrate-like structures in water and their increase at low (supercooled) temperatures [1476, 3625]. d High energy x-ray measurements on supercooled water have shown on deeper supercooling that the intermediate-range order is mainly associated with the growth of a predominantly tetrahedral network out past the fifth shell that is distinctly different from ice-Ih [3549].
The radial distribution function of the O-H and H-H distances
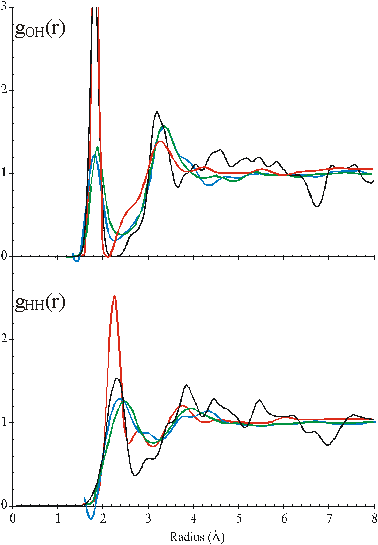
Figure 2. Comparison of the calculated O···H and H···H radial distribution functions of CS (black) with the published neutron diffraction data of water; red [35], blue [17], green [37]. c
The 2.8 Å peak from CS shows 4.34 nearest neighbors, where 0.34 of
these are contributed by the shoulder evident at about 3.2 Å. Thiese details are close to the reported 4.4 nearest
neighbors as calculated from the diffraction data [8], h which also includes the shoulder at 3.2 Å ,as does an ab initio quantum mechanical/ molecular mechanics
molecular dynamics simulation study [922].
The size of the 3.7
Å peak compared to the 2.8 Å peak (0.69:4) from CS is close to that required for the radial distribution function
(Fig. 1). It is also possible that very
weakly hydrogen-bonded molecules may occupy a small number
of the interstitial
sites as found in powdered hexagonal ice [154].
If only 1% of the water molecules occupied such sites, well within the 5% limit [13] possible, this peak would increase by about 50% due to multiple
interactions. The presence of cyclic pentagons increases the
number of second-neighbor distances, at between 4 - 5 Å,
to first-neighbor distances in the ratio of 13.4:4 in contrast
to the 12:4 ratio in ice Ih or ice Ic based structures and the substantially lower ratio
in two-state structures containing ice-two [22]. However, it is pretty difficult
to quantify such ratios as they are entirely dependent on
the cut-off distances used. ![]()
The radial distribution functions of O···H and H···H distances can be calculated from the model (Fig.2). Comparison with the neutron diffraction data is less helpful in testing the model, however, due to the lack of detail in the experimental data, its variability between laboratories, the higher temperatures used (25 °C), the presence of D2O. Also, there are the necessary, but possibly misleading, assumptions that must be made when calculating from the model that the hydrogen bonds are linear and all hydrogen-bonding arrangements are equally probable. However, the model gives H···H peaks at 2.35 Å, 3.9 Å and 4.6 Å with a small peak at 2.9 Å and O···H peaks at 1.85 Å and 3.3 Å with smaller peaks at 4.55 Å and 5.25 Å similar to published data [17, 35, 37].
There is no doubt that all the diffraction data is compatible with the presence of significantly large amounts of tetrahedrally hydrogen-bonded water molecules in liquid water as described in hydrogen-bonding and cluster equilibria.
It should be recognized that the ES clusters will be further 'decorated' by up to 120 H2O molecules around their periphery that will tend to stabilize the cluster by their availability to replace any 'broken' links. In contrast, within the CS structure there is a loosely and strained hydrogen-bonded center with reactive H2O molecules that facilitate the breakdown of the cluster's stronger hydrogen bonds.
[Back to Top ![]() ]
]
Support for the structure of ES comes from its agreement with radial distribution functions of solutions, supercooled water, LDA, and water nano-droplets. Liquid water contains a considerable amount of order that extends almost a nanometer at ambient temperatures [1866]. The cavity-cavity distribution function of supercooled water peaks at 5.5 Å [38], and the neon-neon distribution function in water peaks at 6 Å [38]. Both values are close to the cavity-cavity distribution function peak of ES at 5.4 Å. The radial distribution function of ES around its center consists of several spherical shells surrounding a dodecahedral cavity, where structure-forming ions or solutes may reside. The central (H2O)20 dodecahedron occurs in many places in water science, such as in the clathrate hydrates and their precursor structures, dissolved noble gases, and 2D metal-organic frameworks [3346]. The radius of this dodecahedron is 3.94 Å, agreeing with the minimum cage radius found [39], at 3.9 Å, and the average Kr···O distance found in cold (4 ± 5 °C) aqueous krypton solutions under 110 bar pressure [157]. This last study [157] also gave the Kr···O second shell distance of 6.6 Å in exact agreement with the ES model. The inner four shells of ES, consisting of 160 water molecules (20 H2O at 0.39 nm; 20 H2O at 0.66 nm; 60 H2O at 0.79 nm; 60 H2O at 1.06 nm, see below right), have been found in almost identical positions and orientations within a cavity-encapsulated icosahedral nanodrop of water (see center below) in a polyoxomolybdate (see left below, 20 H2O @ 0.38-0.40 nm; 20 H2O at 0.65-0.68 nm; 60 H2O at 0.76-0.79 nm; 60 O atoms (mostly H2O) in hydrated molybdate at 1.06-1.07 nm) [417]. The stability of the (H2O)100 nanodrop cluster has been confirmed from quantum-chemical computations [1627], and its theoretical infrared spectrum has been calculated [2154]. More details of this hydration are shown elsewhere.
The central 160 water molecules in ES compared with the water in the nanodrop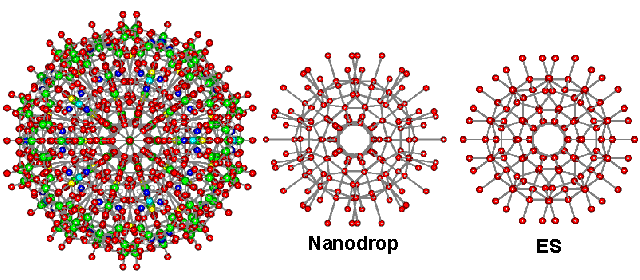
A cluster of silicon atoms (i.e., Si280) with identical icosahedral structuring to ES has been predicted [990a] and found by molecular dynamics [990b] as a stable clustering in nano-sized droplets of liquid silicon with a 15% reduced melting point over crystalline silicon.
Small-angle X-ray scattering (SAXS) has confirmed the presence of density fluctuations in liquid water on a physical length-scale of ≈ 1.4 nm due to fluctuations between tetrahedral-like (ES-like) and hydrogen-bond distorted (CS-like) structures [1604]. [Back to Top ![]() ]
]
When applied to liquids [572], structure, has a different meaning to when it is applied to solids. Liquids are fluids that take the shape of their containers (like gases) but have a nearly constant volume (like solids), varying little with temperature and pressure. Many properties lie between solids and gases but are difficult to model realistically based on those solid or gaseous properties. In liquid water, the molecules have translational motion. However, they may travel in relatively unchanging non-crystalline clusters, containing many water molecules, with far lower hydrogen bond disruption than if the molecules traveled entirely independently (as occurs in gases). Additionally, any rotation of such clusters results in the translation of the individual molecules. Although this requires that long-range order is lost, there is still some short-range order. This short-range order extends to at least 8 Å radius even with totally inert, nonpolar, and spherically symmetrical molecules such as in liquid argon [95], and up to 15 Å radius (equal to the proposed ES structure) in the more-ordered supercooled heavy water (D2O) [221]. The distance over which this short-range order exists is greater when there is extensive hydrogen bonding as in water. This has been confirmed in aqueous dipole moment calculations where water 10 Å distant still contributes significantly [452]. In simulations, even where the orientation of individual water molecules is rapidly lost, coherent (orderly k) patterns of extensive hydrogen bonding have been found to exist for periods lasting throughout the simulation [329]. In liquids, the X-ray (and neutron) diffraction pattern corresponds to the time-averaged positions (with exposure times for X-ray studies many orders of magnitude greater than the longest simulation) of the molecules within the volume corresponding to the potential range of this short-range order and so can give valid information as to the preferred structuring of these molecules. An alternative way of looking at this structure is as the average, directionally correlated, network around the water molecules taken from an extremely large pool of liquid water molecules; many orders of magnitude higher than used in simulations. In this context, it is relevant to note that the relative positioning of water molecules around cations such as Ca2+ remain close to fixed essentially forever but with individual water molecules exchanging with the bulk in less than a nanosecond. Also, hexagonal ice remains firmly ordered and crystalline despite continually and rapidly breaking and changing its hydrogen bonding. There is evidence that water structuring may change over periods greater than seconds [631] or days [1102] or, in other studies, at least 1016 times greater than the lifetime of an individual hydrogen bond [4, 509, 1148]. Another research study shows that disturbances in the structure of single water molecules may last only 50 femtoseconds due to the rapid redistribution of energy amongst the cluster hydrogen bonds [750]. Thus the structure determined for water depends on the time- and size-scales over which it is determined.
It is also possible that there may be more than one stable or metastable liquid structure coexisting in equilibrium simultaneously. This has been shown for several materials, including mixed oxide melts [768], liquid sulfur [769], and liquid phosphorus [770]. Note also that there are many instances where two liquid water phases coexist in aqueous biphasic systems.
The explanation for many anomalies given by Shi, Russo and Tanaka in 2018 [3503] involves a dynamical mixture of two states for water; a low-temperature ordered state based on the (H2O)5 tetrahedron (S) and a high-temperature disordered state based on a slightly distorted (H2O)5 tetrahedron plus a close additional sixth H2O molecule (ρ).
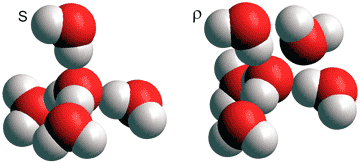
Note the similarity of these two states to the primary states of ES (S) and CS (ρ). Considering water as a dynamic mixture of these two structural types allowed the explanation of thermodynamic and kinetic anomalies due to their temperature and pressure dependence [3503]. [Back to Top ![]() ]
]
There still seems doubt in the minds of some workers as to whether
the radial distribution peak at about 3.7 Å exists [1788b],
despite the need for water molecules at about this distance to give water a higher density than ice. Narten et
al. [9] first
reported this peak and explained it in terms
of interstitial water molecules within ice Ih type hexameric
boxes. He later put this peak down to artifactual ripples
due to the early termination of a Fourier integral [58],
and therefore this peak has no structural significance. The peak
was later again observed in his neutron diffraction data [35].
The X-ray data have been reanalyzed, and the peak
is still present [59],
as it is in some simulation studies [7, 66] and the neutron diffraction
of effectively-powdered hexagonal ice [154]. It has also
been shown to grow with increasing temperature [50]
and pressure [51]. Four water molecules are generally found roughly tetrahedrally placed in supercooled water at distances about 2.78 Å. The position of the fifth nearest water molecule has been located using simulations and appears maximally at about 3.8 Å and 3.0 Å, in relative amounts dependent on the density [1055]. 2009 X-ray evidence has established the presence of fine structure at about 3.4 Å that is not due to artifacts [1631, 1788a/c]. It
is now the majority view of researchers in the field that
water molecules exist at these intermediate distances in liquid
water under ambient conditions [1756]. They would be at about
the expected distance for non-hydrogen-bonded inner-sphere
water molecules. [Back to Top ![]() ]
]
The data obtained by both X-ray and neutron diffraction (for a review, see [392]) are subject to uncertainties. The radial distribution function of the oxygen atoms is obtained from neutron diffraction data by subtraction of the hydrogen (deuterium) intensities, thereby giving rise to noise, which, when smoothed, leaves only the most significant features. Also, neutron diffraction data is generally analyzed, ignoring any inherent differences in the water structuring between D2O, HDO, and H2O and, therefore will produce less detail as these structures differ significantly. Even small differences in the H2O content of D2O give rise to very different radial distribution functions [715], a problem made worse at low temperatures. Thus, there are reasons to suppose that mixed D2O, HDO and H2O solutions are not entirely homogeneous. It is particularly noticeable that the reported radial distribution functions of the oxygen atoms, determined from neutron diffraction data, differ considerably from each other. Also, the structures of identically produced low-density amorphous ices of D2O and H2O are not identical, even allowing a temperature shift [940]. A useful review of these techniques has been published [916].
X-ray diffraction is sensitive to the concentration of electrons.
These are assumed to be spherically distributed
during analysis, but as the molecule is not spherically symmetrical, clearly this is an approximation. However, the electron densities around the hydrogen atoms are
displaced somewhat towards the oxygen atoms. Also, the electron distribution
around water molecules in liquid water appears to be more
spherical than in the gas phase [90]. Any residual effects that this causes are primarily confined
within the nearest-neighbor shell [59].
The data (for the radial distribution function of water) is
not subject to the same amount of noise (and required smoothing)
as with neutron diffraction and is intrinsically capable
of showing a greater degree of fine structure (see for example
the comparison of X-ray and neutron diffraction data given
in [888, 1245]). Although
the fine structure in the X-ray data of Narten [9]
was later interpreted [58] by Narten as 'ripples' due to the data processing, the key peak
at about 3.7 Å has now been established present beyond
question. It seems as if such 'ripples' are of importance,
mainly below 2.5 Å. An X-ray scattering experiment
at 27 °C reported far less fine structure [199], as does a detailed analysis of X-ray diffraction data at ambient temperatures [1971]. However, the data does still show agreement in terms of the broad shells out to the 5th. The higher temperature and the greater inherent 'smoothing' may be responsible for the differences, as work at lower temperatures certainly shows fine structure out beyond 1 nm [1476]. In 2011, wide-angle X-ray diffraction measurements with high energy-resolution resolved a shell structure out to about 1.2 nm [1755] even in ambient and hot water but contributed by a minority species. [Back to Top ![]() ]
]
The term 'interstitial' can have several meanings.
Historically it meant unbonded or weakly hydrogen-bonded water
molecules sitting in the empty spaces in a tetrahedrally bonded
network, such as within the hexameric
boxes in ice Ih structures [9]
(this is the meaning that is generally used on this site).
More recently, the term 'interstitial' has been used to describe water molecules
that cause the 3.7 Å peak of the oxygen radial distribution
function. They may be in this position because they are (i) not
hydrogen-bonded, (ii) tetrahedrally hydrogen-bonded
but in a separate local cluster, or (iii) hydrogen-bonded within the same local cluster but where there is a considerable bending of the hydrogen
bonds involved. These definitions are not necessarily
mutually exclusive. It is not the case that interstitial molecules
must have no hydrogen bonds; it is possible that
such a molecule can have some normal or somewhat distorted
hydrogen bonds. The idea of interstitial molecules has
been re-introduced using the evidence of some simulation studies
[66], the neutron diffraction
finding of interstitial water in effectively-powdered hexagonal
ice [154], and modeling from water's proton nuclear magnetic resonance (NMR) [4058]. When
liquid water is put under pressure, there appears to be an
increase in the interpenetration of hydrogen-bonded networks at
about 200 MPa (at 290 K) as evidenced by the increase in
the O····O nearest molecule separation
distances, and O-H stretch vibration frequency with pressure
between about 200 to 400 MPa [533].
Both isoelectronic neon and the larger argon atoms can be
found in interstitial sites in hexagonal ice, proving they
have sufficient size to contain water molecules. Ice-seven and ice-eight both consist of
interpenetrating networks where all water molecules effectively
occupy interstitial sites. [Back to Top ![]() ]
]
There are many examples of the formation of dodecahedral clathrates in aqueous solutions [26, 27]. Dodecahedral clathrates can form with small molecules including the noble gases (except for helium, which is too small), NH4+, H3O+, Cs+, N2, O2, CH4 [349], H2S, CO2, (H2)2 and (H2)4, C2H6, C3H8, Kr, and Xe [2850]. Where formed, the stability of the (poorly formed) crystals depends on the pressure (generally greater than 1 MPa). Clathrate clusters have also been proposed to contribute to why anesthetics like chloroform and nitrous oxide have their action [733]. Dodecahedral clusters containing NH4+, K+, and Cs+ have also been found in ionized liquid water in the gas phase by mass spectrometry [26; see also magic number ions]. Such cavity formation is natural in water, increasing the hydrogen-bonding strength in their neighborhood [31]. The Hofmeister series, whereby ions affect the stability of proteins in solution by either creating or destroying the structure of water, may be explained in part by how well large ions may sit passively in the dodecahedra, stabilizing ES, relative to how strongly they create their environment [40]. Cations that stabilize proteins in solution also create low-density water [29]. Theoretical studies have shown that the full icosahedral cluster (H2O)280 and, to a lesser but still significant extent, the central (H2O)100 core both stabilize the central dodecahedral cluster (H2O)20 and help stabilize the formation of clusters with contained molecules (i.e., clathrates) [1619]. There are some unusually strong hydrogen bonds, due to cooperativity, in particular (H2O)20 clusters where the hydrogen bond energy was calculated using symmetry-adapted perturbation theory. In liquid water, such hydrogen bonds were found to be more than three times stronger (-82.28 kJ ˣ mol−1, 1.42 Å long) than a typical hydrogen bond [4035].
The most prominent bands in the experimental vibrational spectra of the low-temperature water component are peaked near 200 cm−1 and 3400 cm−1 and resemble those observed in ice and solid clathrate hydrates [3122], in agreement with those expected from the icosahedral cluster ES. Using 2-D IR spectra, it has been concluded that transient pentameric rings and their fused structures form major components in liquid water [3462]. These results are consistent with the hypotheses that the population of clathrate hydrates increases with the lowering of temperature, and higher density water may contain collapsed clathrate structures.
The radial distribution function of TMACl compared to the model
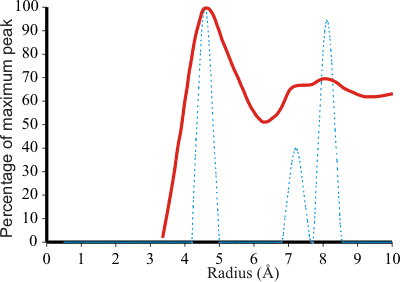
The tetramethylammonium ion (TMA) is most effective [29] at stabilizing proteins, and its effect on the structure of water has been investigated. i In ES (dotted blue, right), expansion of the inner cavity to a radius of 4.60 Å, due to charge or steric effects, causes the next two shells in ES to expand to 7.23 Å (smaller peak) and 8.13 Å (larger peak). These three peaks may be related to those found at 4.6 Å, 7.2 Å (smaller peak) and 8.2 Å (larger peak) around the tetramethylammonium ion of 0.5 M TMA+Cl− in D2O (solid red, right) [39], as the 4.6 Å radius for the dodecahedral cavity is identical to half the sum of the TMA ion (6.34Å) [545] and water molecule (2.85 Å) diameters. This clathrate formation was first described by Frank and Wen in 1957 [97]. Raman analysis has shown that the strong hydrogen bonds in aqueous R4NCl solutions at low temperatures are due to clathrate-like structures [2439]. These strong hydrogen bonds have been confirmed from isothermal compressibility studies [3329]. Furthermore, TMA solutions increase the solubility ('salt-in') of small hydrophobes [1789] in agreement with the expectation from the ES model. Together with the slightly larger tetraethylammonium ion, tetramethylammonium ions are distinctly hydrophilic, whereas the larger tetraalkylammonium cations are much more hydrophobic [3143]. This is likely due to the energetic cost of fitting the larger ions into clathrate-type structures.
The ES structure provides about 1.4 dodecahedral sites per molecule
for a 0.5-M solution. When higher concentrations of TMA+Cl− were used, demanding more dodecahedral sites than those that ES can
provide,
the neutron diffraction peak detail was lost. In solutions
of TMA+Cl−,
the chloride had a coordination number to the water of five and
the TMA+···Cl− distance was 5.3 Å [39]. Both
agree with the chloride ion sitting asymmetrically in a nearby
pentagonal box to a TMA ion situated within a dodecahedron, as this gives a coordination
number of five to a dodecahedral face and a TMA+···Cl− distance of 5.34 Å, given a (reasonable) H2O···Cl− distance of 3.24 Å. This study [39]
also showed little effect of salt on the structure of
water despite the presence of water dodecahedra, which strengthens
the argument that such dodecahedral structures are present
in pure water. Analysis of the hydrogen bond angles indicates
an increased degree of orientational ordering comparable to
that occurring in water over 20 °C colder [211].
At high salt concentrations, where more than one dodecahedral
site is required per 70 water molecules, other sites may
arise from tessellated, if distorted, dodecahedra with five water
molecules per dodecahedron site, and 6.1 Å between interstitial
sites. Alternatively, a tessellated structure may form from dodecahedra separated by single pentagonal boxes
(25 water molecules per dodecahedron site, as may be present
in aqueous dimethyl sulfoxide (DMSO) solutions [342]. This has
10.6 Å between large interstitial sites and 5.3 Å between large and small interstitial sites. This latter structuring
may also be indicated at the phase transitions noticed in
concentrated salt solutions (≈ 2M) [556],
due to the ions breaking through their solvent-separated hydrated
structures. Microwave dielectric relaxation measurements have
indicated a critical behavior of water at a mole fraction
(xw) of 0.83 [6].
This can be explained by tessellated
water dodecahedra, which have the required number of interstitial
sites per water molecule (xw = 0.83). [Back to Top ![]() ]
]
The radial distribution function of LDA II from [2415]
compared with ES model
![Comparison of the radial distribution functions of LDA II from [2415] and those of the ES model Comparison of the radial distribution functions of LDA II from [2415] and those of the ES model](images/LDA.gif)
LDA is expected to be thermodynamically continuous with liquid water [16], and it certainly gives a similar diffraction data [43] (see the comparison of LDA [2415] and ES, right) and tetrahedrality [2143] to supercooled liquid water, with identical tetrahedrality on entering 'no man's land' (≈ 227 K) [2143]. Many of the properties of LDA are those of quasicrystalline material (see [1178]) that would be expected from ES, with its hexagonal and cubic ice substructures. The radial distribution functions of ES show similarities to those of LDA, with both including features similar to cubic [175] and hexagonal ices [41, 1155]. Also, LDA shows crystalline-like behavior in its physical properties (thermal conductivity [617], inelastic incoherent neutron scattering [41], and dielectric relaxation [1155]) with strong similarities to hexagonal and cubic ice [1155]. Neutron diffraction data have been used to suggest the presence of pentamers, boat and chair hexamers, and partial dodecahedra [42]. LDA gives an O···O radial distribution function with peaks at 2.79, 4.56, 6.95, and 8.60 Å from X-ray data [43a] (2.75, 4.5, 6.5, and 9.0 Å from [3501]) whereas the ES gives peaks at 2.80, 4.57, 5.38, 7.06, 7.93, 8.88, and 9.16 Å which reduce to just four peaks at 2.8, 4.6, 6.7, and 9.0 Å, on Gaussian broadening, showing close agreement. The neutron diffraction data [20] gives peaks at 1.8, 2.3, 3.3 (shoulder), 3.8, 4.6, 5.2 (shoulder), 7.7, 8.4, and 9.1 Å and troughs at 2.7 and 6.4. Å. This compares favorably with the calculated distribution function from ES, which gives peaks at 1.8, 2.3, 3.2, 3.8, 4.6, 5.3, 7.3, 8.0,and 9.2 Å and significant troughs at 2.8 and 6.8 Å. This material has the same density [34] as ES and probably bears some relationship to it, particularly as clusters with icosahedral symmetry cannot form crystals and therefore must form amorphous solids or quasicrystals.
The similarities between ES and LDA are reinforced by the deformation and diffusive behavior of LDA as a viscous liquid rather than as a solid ice [334]. The phase transitions found by some in supercooled water [44, 45] may be due to the same reasons as the sharp transition between the puckered (CS) and non-puckered (ES) water clusters seen in the molecular mechanics optimizations; the ES structure showing both the perfect tetrahedrality and possessing precisely four nearest neighbors b as found to be required by modeling [498]. A study of homogeneous nucleation rates in supercooled water has found two rate constants. The slower one can be assigned to nucleation of the more strongly hydrogen-bonded ES and the faster one to CS nucleation [333]. An ordered arrangement of cavities has been proposed from the diffraction data of LDA [30], also in agreement with the ES model. It has been reported that the entropy of LDA is only a sixth of that than can be explained by a random network model [21] but in good agreement with the much more ordered ES. A Raman spectral study of LDA showed at least two or possibly three, distinct species [46] in line with three in the ES model. Raman spectra have also shown the similarity between LDA and glassy tetramethylammonium chloride solution [167], a proposed ES-like structure (see above). Further support for an ordered (for example, ES-like) model for LDA has been given by inelastic neutron scattering [175]. Maximum tetrahedrality in liquid water has been found at 229.2 K for H2O and 234.5 for D2O [3134]. At higher temperatures (about 80 °C), the structuring goes from being mainly tetrahedral with four hydrogen bonds (tetrahedrality = 1) to mostly tetrahedral but with only two hydrogen bonds (tetrahedrality = ½) [3404]. LDA-nanodomains form with radii of about 0.8 nm in eHDA below about 0.2 GPa. These are similar in size to the (H2O)100 clusters [3162] found within ES. There are also similarities between HDA and CS-like structures in terms of local geometries involving pairs of molecules separated by multiple hydrogen bonds [4358]..
Methane within a clathrate shell
Clathrate-like structures (for example, see right) are here proposed as being part of water's natural structure, albeit in a mainly puckered state at ambient temperatures and increasingly fragmented at higher temperatures. Several Raman and X-ray diffraction studies have established local convex clathrate-like structures at atmospheric pressure, which become increasingly important as the water is supercooled [195], or under the influence of infrared radiation [730] or sunlight [1173]. This clathrate formation at low temperatures has been proposed as being responsible for many of the anomalous properties of water [195]. Clathrate hydrate formation overrides hexagonal ice formation in supercooled solutions [1656]. Molecular dynamics simulations agree, showing that clathrate cages have longer lifetimes at lower temperatures [662] and that sub-clusters of ES are found in supercooled water [729]. The degree of tetrahedral hydrogen-bonding also increases on supercooling as the average water cluster grows [658, 1601]. The proportion of water molecules connected by 4- and 3-hydrogen bonds in supercooled water (250 K) has been calculated, using an atoms-in-molecules approach, to be 41% and 29%, respectively [1531]. If liquid water at this temperature consisted of a close-packed ES,arrangement, it would contain about 42% (4-hydrogen-bonded water) and 32% (3-hydrogen-bonded water) in close agreement. e Further support for such clustering is that low-density water has been shown to exist around aqueous cavities [1080] and that the resistivity of water increases considerably at low temperatures. Shear viscosity and self-diffusion studies have demonstrated high concentrations of clathrate-like structures in supercooled water [47]. In particular, water was shown to diffuse through many hydrogen-bonded water pentagons, such as occur through the spines of ES, where all water molecules line pathways of large cavities, separated by pentagons. The number of water pentagons required to explain water's anomalies (≈ 0.13/mol) is almost exactly equal to the number in ES (36/280; 0.129/mol) at the homogeneous nucleation temperature [366]. Using wide-angle X-ray scattering, the structural changes of water upon deep supercooling down to 228.5 ± 0.6 were studied in 2021 [4386]. Local ordering resembled that of low-density amorphous ice and consisted of a pentamer-based hydrogen-bonded network (as the ES model) distinctly different from that of hexagonal ice.
Vicinal water,
extending for tens of nanometers but well within the unstirred 'Nernst'
layer near inert solid surfaces, has been found to have properties
consistent with partial conversion to low-density
water; for example, reduced density (-4%) and raised dielectric,
specific heat (+25%), compressibility (+20-100%), and viscosity (+200-1100%)
[205]. The thermodynamic
rationale for the formation of this (interfacial) vicinal water
is that the loss of hydrogen bonds at the surface increases the
enthalpy so necessitating the water molecules to compensate by doing
pressure-volume work. That is, the network expands to form
low-density water with lower entropy (see also hydrophobic
surfaces and for example, [480]). [Back to Top ![]() ]
]
Flicker noise spectroscopy indicates the presence of (H2O)280 clusters at low temperatures [773]. Vibrational spectra have shown the presence of both large clusters (about 240 molecules) [18] and cyclic water pentamers [48, 3462], in agreement with CS. At low temperatures below 0 °C, water is mainly found in hexagons and pentagons with large fused pentameric structures, including the clathrate dodecahedra ((H2O)20), dominating [3462], in agreement with the ES structuring that consists only of these clusters [3281]. Puckering of the pentamers was found to increase with temperature [48]. Simulations in 2014 indicate a two-state structure where the low-density state has progressively more pentagonal (H2O)5 rings as the temperature is lowered, increasing to 34% at 200 K and comparing favorably with 50% present in 'pure' ES [2127]. In addition, quantum delocalization of hydrogen-bonded protons between oxygen neighbors occurs in the pentamer, but not the hexamer [2726]. Such aromatic-like delocalization, within the aqueous pentamers and dodecahedra present in supercooled water, stabilize their structures and contribute to the stability of ES-clustering, where half the water molecules are within pentamers.
Some facts support the presence of some very bent weaker hydrogen bonds in the structure of water. These include (i) the high ice-water energy of fusion, which has been suggested as due to the weakening of a proportion of the hydrogen bonds due to their distortion, and (ii) the vibrational Raman spectra [35] that indicate a range of weaker hydrogen bonds. Mid-IR pump-probe spectroscopy of HDO in D2O has confirmed the existence of two distinct molecular species in water due to their orientational relaxation times as would be expected in the strongly-hydrogen-bonded ES and weakly-hydrogen-bonded CS clusters [189]. In particular, the difference in energy between these forms can be deduced from both the Raman scattering in the O-H stretching region and the O-H overtone infrared region to be about half the energy of a hydrogen bond [210]. Factor analysis of the infrared spectra of H2O and D2O both show two (and only two) fully hydrogen-bonded species in equilibrium, with their relative concentrations changing with respect to temperature; one predominant at low (supercooled) temperatures and the other at high temperatures, with a 50% crossover at about 30 °C [1502]. The transition from CS to ES can explain the high root-mean-square fluctuations of the intermolecular energy in liquid water (7 kJ ˣ mol−1) and the fragile-to-strong a transition in supercooled water at about 225 K [1040] and close to the second critical point. This has been confirmed by a molecular dynamics study suggesting that liquid water consists of both high-density and low-density amorphous-like regions with a transformation between them in supercooled water [172]. It has been proposed that the observed heat of fusion (6.0 kJ ˣ mol−1) is due solely to an increase in bond bending going from ice to water [49]. The average root-mean-square distortion occurring in CS is 13.7°, which gives a very close value (5.2 kJ ˣ mol−1) to this observed heat of fusion and agrees with the 16° distortions estimated from the 600 cm−1 libration band [47]. High-resolution oxygen K-edge X-ray emission spectra (XES) of liquid water showed two distinct narrow lone-pair derived peaks, assigned initially to tetrahedral and strongly distorted hydrogen-bonded species, as expected from ES and CS structures respectively, with no intermediate structures [1557]. Although these results were shown to require a more elaborate explanation [2419], a later analysis reaffirmed the original assignations [3366]. However, this result remains disputed [3570].
Percentage of the low-density state of water with the temperature
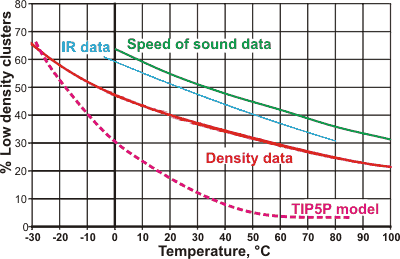
The percentage composition of the low-density state of water as determined by the variation in density [1354 ] (red line, also agreeing with viscosity and refractive index data), IR absorbance data [1738] (blue line), speed of sound data [3086] (green line), Raman data [4485] (purple line) and from the TIP5P model [3238] (magenta dotted line). The %-low density water controls the anomalous behavior. The four data lines are pretty close, considering that they are from different laboratories using very different data. The differences between the lines may be explained due to the two 'states' of water not being precise structural forms but mixtures of related structures and that the necessary peripheral hydrogen bonding around the clusters has different effects. The TIP5P model shows other deviations at higher temperatures, and is similar to the data derived from x-ray scattering [4486]. Other models give far lower curves (e.g., [4122]).
Although still not universally accepted, f there have been a growing number of papers (and research groups) proposing a two-state mixture model to explain many of the properties of water [23, 24, 25, 56, 57, 262, 268, 276, 409, 699, 826, 1150, 1334, 1353, 1354, 1588, 1595, 1603, 1604, 1612, 1639, 1640, 1674, 1691, 1738, 1757, 1763, 1859, 1909, 1980, 1996, 2019, 2051, 2089, 2127, 2129, 2144, 2189, 2295, 2218, 2295, 2341, 2505, 2569, 2602, 2653, 2658, 2727, 2755, 2794, 2890, 2918, 2925, 2930, 2972, 3014, 3086, 3111, 3122, 3162, 3203, 3238, 3284, 3296, 3317, 3355, 3358, 3363, 3455b, 3503, 3607, 3635, 3654, 3660, 3696, 3851, 3959, 4000, 4054, 4076, 4094, 4122, 4461]. Although these papers do not use the same structures for the two states, they utilize overlapping ideas. The ES-CS model agrees with the 2-state model put forward in 2018, in that the ES structure shows a clear separation between the first and the second shell of nearest neighbors, and the CS state characterized by a disordered arrangement of second-shell molecules [3256].
The experimentally determined thermal evolution of the O-H stretch vibration band shows low and high density (0.94 g ˣ cm −3 and 1.15 g ˣ cm −3) hydrogen-bonded structures, whose relative content oscillates. The low-density and high-density hydrogen-bonded structures have been shown to exhibit different susceptibilities toward the alignment imposed by the external field due to variation in local hydrogen bond strength [4054]. A parameter-free structural indicator was developed in modeling studies that classified the local environments of water molecules in stable and supercooled liquid states, revealing a clear two-peak distribution of local properties [4000]. The predominant forms, at supercooled temperatures, were tetrahedrally coordinated and resemble the structure of LDA.
The NMR spectra of supercooled water droplets produced on cooling solutions of water perdeutero-toluene (toluene-D8, 1:500) to below 0 °C were examined [3970]. Two well-separated proton peaks were found corresponding to low-density strongly hydrogen-bonded water clusters and bulk-water-like domains. Furthermore, the amount of low-density strongly hydrogen-bonded water clusters was greater below about 250 K. All local water structures converge to solely the low density form at about 225 K.
A two-state mixture model has been used to construct an equation of state for supercooled water in the official guideline on thermodynamic properties of supercooled water [2089]. Miscible liquids like water and alcohols or just water as here, may coexist in equilibrium with nanoscopic, but without macroscopic, phase separation [2235]. Many water anomalies arisie from a competition between two local structures: a low-density, ordered structure and a high-density, disordered one. Also, aqueous solutions of 'miscible' solutes may give rise to mesoscopic near-spherical Brownian aggregates with diameters from a hundred to a few hundred nm, showing the presence of separated two-state aqueous systems [1725]. Molecular dynamics simulations have shown that while the first coordination shell contracts upon cooling at a constant volume, the second shell expands (negative thermal expansion) [3203]. Coherent X-rays have shown that increased tetrahedral clustering causes significant effects on the ultrafast water dynamics at low (supercooled) temperatures [3369]. A model used successfully for comparison with the experimental data utilized dodecahedral template structures; these dodecahedral structures were unstabilized forms of the key stabilized feature in the ES structure [3661]. All these proposals are consistent with the ES and CS cluster model.
The significant increase in the resistivity (= 1/conductivity) of water at low temperatures [737] indicates the increased formation of localized and limited isotropic hydrogen-bonding, preventing lengthy directed proton movements. Furthermore, the electrical conductivity of water, which increases on degassing [711, 4347], j also supports this view, as dissolved nonpolar gases promote the formation of ES clusters at low temperatures.
The existence of such equilibrium also enables an explanation of the way some organisms produce low-density water to protect against desiccation [278] and high temperatures [279] and pressures [280]. More ES clusters are found on irradiation with sunlight [1589 ], probably due to a combination of more structured water-absorbing light at about 270 nm [1328] and interactions with the evanescent wave.
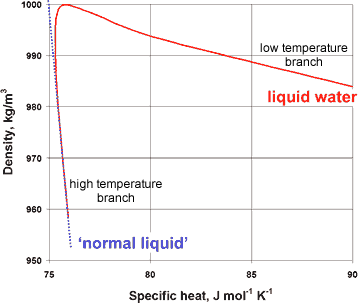
Variation of specific heat with density for liquid water
Variation of viscosity with density for liquid water
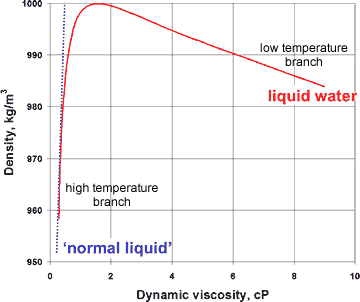
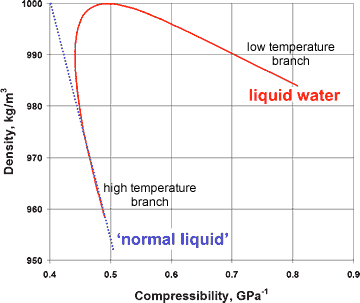
The presence of a hybrid two-liquid miscible system can be shown more dramatically from the changes in the compressibility, viscosity, and specific heat with the density of liquid water (at constant pressure), where the properties of liquid water can clearly be seen to tend to different behavior at the extremes of the parameters (see right and below).
Variation of compressibility with density for liquid water
The minimum number of possible of hydrogen bond arrangements in the fully occupied low-density icosahedral network (ES) is 2130 ˣ 712 (curiously this number equals close to 1.50280) as determined during the molecular building. This is in agreement with the minimum entropic factor expected of 1.5 structural variations per water molecule [8]. The icosahedral symmetry of the water clusters fits well with the expected symmetry of disordered systems such as liquids [3699].
In modeling studies, the thermodynamic anomalies of supercooled water appear to occur in a well-defined metastable liquid state separated from the crystal by a substantial free energy barrier [2919]. This is in agreement with the expectation of the ES model.
The cluster size (about 2.8 nm diameter) is close to that found (about 3 nm diameter [140]) to be the limit below which crystalline components in aerosol ice clusters cannot be found and also close to the critical bubble volume found by acoustic cavitation in cold water [1642]. A pronounced peak at a slightly greater diameter (about 3.4 nm) has been observed in aqueous aerosols using a differential mobility particle sizer [141]. Also, a peak at about 3 nm diameter is found in negatively charged waterfall aerosols [2049]. A similarly sized cluster (about 2.5 nm diameter) has been found in negatively charged nanodroplets formed from splashed water [1477]. The internal hydrogen-bonding in such droplets is thought to reduce evaporation and prolong the droplet lifetime. A similarly explained cluster (3.4 nm diameter) has been found as an icosahedral aqueous cluster of thirteen fullerene C60 molecules [271]. Also, the same length scale has been found in an exciting experiment [912], where a tiny water pool (about 10−23 L) is stretched between hydrophilic surfaces using an atomic force microscope. The thread of capillary meniscus water has its final "sticking" position at 3.1 nm and breaking when 4.2 nm long and 2.6 nm wide and with "sticking" steps roughly equivalent to the icosahedral water cluster cavity positions. The existence of stable, nearly stationary ES-like states in ambient and supercooled water on the nanometer length scale and the time scale up to ~ 0.5–1 ps has been predicted using a mode coupling theoretical approach [4288]. A diameter of about 2 nm has been determined for water clusters in cold water using acoustic phonons (packets of energy) [1162]. This is also the minimum diameter for nanodroplets before the homogenous bulk nucleation limit for ice formation [4394]. When the structures of ice-amorphized, supercooled water, approximately-spherical, nanodroplets are examined within 'No man's land' (≈ 150-235 K), it is found that the center of the tiny droplets (N ≽ 360 molecules of H2O) are formed of isotropic low-density water (but not crystalline ice) as might be expected if they were derived from similar to ES [3060]. Similar results have been described by another team [3336]. A rationale for the preferable formationof cubic ice from supercooled water is that the hydrogen-bonded clusters present in supercooled water adopt conformations more similar to those in cubic ice [3667]. This would confirm the extensive presence of the all-gauche ten-molecule tetrahedra in the ES cluster fragments thought to be formed with supercooling. Using molecular dynamics simulations of TIP4P/2005 water model, it has been found that liquid water's oxygen atoms become more orientationally ordered with cooling and, at temperatures less than 230 K, its orientation is ice-like [4269].
The proposed structure fits the much-promulgated theory of how sugar molecules interact with water, based on anisotropic hexagonal ice-type interactions [5, 52], but allows sugars a wider range of orientations. Thus, in a solution of scylloinositol, each hydroxyl group can donate and accept a hydrogen bond so long as the scylloinositol is situated in one of the 80 chair-form hexagonal sites with different orientations within each 280-molecule cluster. Thus many sugars can create locally stabilized areas within the network of icosahedral clustering. ES may also be formed as a significant part of the low-density water reported developing in gels and at the surface of some macromolecules [4]. An orientation effect may be expected to strengthen the hydrogen bonding in the water.
[Back to Top ![]() ]
]
Fragile-to-strong behavior
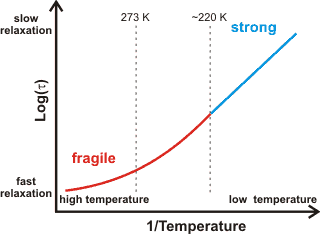
a The fragile-to-strong transition. Fragile liquids, such as liquid and mildly supercooled, water (higher density, more fluid), have a large heat capacity and exhibit non-Arrhenius behavior. This non-Arrhenius behavior is where the log(viscosity) varies non-linearly with the reciprocal temperature, see right. The structural relaxation time (τl ) is a constant related to the viscosity. The degree of fragility may be quantified [2970]. T0 is the Kauzmann temperature where the divergence from Arrhenius behavior (see below) occurs [1078]) due to the molecular structuring changing with temperature [1075]. Fragility can be a consequence of clustering producing no long-range density ordering.
Strong liquids, such as deeply supercooled water (low-density, less fluid),
have a small heat capacity and exhibit Arrhenius behavior (that is, log(viscosity) ![]() 1/temperature with their graph showing a straight line);
1/temperature with their graph showing a straight line);
![]()
where the structuring changes little with temperature [232], and the density fluctuations are minimal. Deeply supercooled water is the strongest liquid known, with such behavior being very unusual for a hydrogen-bonding system. Quantum fluctuations, due to the strong hydrogen-bonding but light hydrogen atoms, play a vital role in the dynamics of this profoundly supercooled water, ≈ 136 K [2971].
Fragile liquids, such as normal liquid water, have curved lines (of log(viscosity) versus 1/temperature). The viscosity is insensitive to temperature in the hot liquid and strongly dependent on temperature in the cold liquid. The fragile to strong crossover has been suggested as a smoking gun for the existence of a liquid-liquid critical point in water, both in the bulk phase and also in solution [3110]. The apparent fragile-to-strong transition in water (at about 220-225 K [1040, 1078, 1200]) has been explained [558] as being a consequence of the balance between hydrogen-bonding effects (low entropy found in low-density water) and the van der Waals dispersion forces (higher entropy) being disturbed in favor of the hydrogen-bonding alone at lower temperatures. Thus, it can be supposed that there is fully tetrahedral clustering at these lower temperatures with no interstitial or interstitial-like water molecules. [Back]
b There is a measure of uniformity (τ) in the H2O-H2O hydrogen bond lengths (the translational order parameter, and the degree of order in the local density) in the same way that tetrahedrality measures H2O-H2O-H2O angle uniformity. The density order parameter ![]() where ξ = rρ3 and r = the O···O distance, ρ is the density, ξc is a suitable cut-off distance [1082]. The density order tends to a minimum as the tetrahedrality tends to a maximum. [Back]
where ξ = rρ3 and r = the O···O distance, ρ is the density, ξc is a suitable cut-off distance [1082]. The density order tends to a minimum as the tetrahedrality tends to a maximum. [Back]
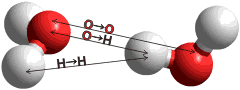
Tetrahedral H-bonded water pentamer
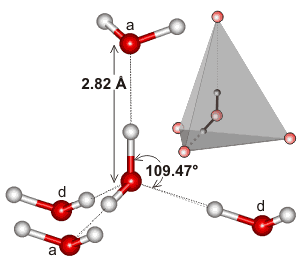
c Note that the prominent peaks indicate that the principal feature in liquid water (as in ice) is a water molecule at the center of a tetrahedron of water molecules with O···O ≈ 2.8 Å and ≈ 4.6 Å, O···H ≈ 1.8 Å and ≈ 3.3 Å and H···H ≈ 2.4 Å and ≈ 3.6 Å. There is no difference between the acceptor (a) or donor (d) hydrogen-bonding water molecules. Peaks due to O-H (≈ 1.0 Å) and H···H (≈ 1.6 Å) distances within the same molecules are always excluded from such analyses. [Back]
d Although this reference [1476] discusses additional clathrate structures, the icosahedral clusters addressed here also contain an O···O radial distribution maximum at ≈ 1.06 nm and are supported by the data presented, with the maximum ≈ 1.08 nm. [Back]
e Calculated using 74% close-packing and hydrogen-bonding numbers as calculated from the ES structure and shown on another page. [Back]
f A two-dimensional Raman-terahertz (THz) spectroscopy study [2050] at about 25 °C, sometimes cited as non-supportive of the two-state mixture model, rules out persistent structures but does not invalidate cluster formation and supports heterogeneities in water. Several molecular dynamics simulations (such as [2686] fail to show two-state mixture models, but this may be due to the failure of the models used (TIP4P/2005) to predict many of water's properties. Small-angle X-ray scattering data, taken together with water molecular simulations, showed no support or need for 2-state heterogeneities in water structure at 25 °C [1520], but this is higher than the low or supercooled temperatures where water anomalies are most apparent. A 2016 study combines the two-state mixture model with a continuum model [2696]. Small-angle neutron scattering data has been used to present a possible explanation of water anomalies that do not involve large-scale heterogeneities or critical behavior [3322]. Quantitative X-ray spectroscopy has been shown to be compatible with continuous distribution models of water under ambient conditions [3670]. Although this discussion shows that the two-state mixture model is not necessary to explain the spectra, it fails to rule it out, and their results may be due to structural averaging. Resonant inelastic x-ray scattering of water can be used to support either or both the two-state mixture model and the continuum model but both with a major feature of tetrahedral hydrogen bonding [3720]. Chandler's several papers denying the two-state mixture model (e.g., [2144 b,c]) have now been proven to be mistaken and misleading [2144 e,f, 3420]. [Back]
g The radial distribution function g(r) represents the probability of finding a neighbor at a center-to-center distance between r and r + δr. gOO(r), gOH(r), and gHH(r) represent oxygen-oxygen, oxygen-hydrogen, and hydrogen-hydrogen pairs, respectively, usually with the probability related to atoms from the same molecule being subtracted (for a review, see [2167]). [Back]
h A common error is to state that these 'nearest' water molecules are hydrogen-bonded to the central water molecule, whereas less than four molecules are hydrogen-bonded, with the remainder being unbonded neighbors. [Back]
i Tetra alkyl ammonium halides have a tuneable hydrophobic/hydrophilic nature because of the possibility of changing the cation alkyl chain length [3286]. [Back]
j It is suggested that carbonic acid may increase in frozen samples (produced by freeze-thaw degassing) at the cost of any dissolved CO2 [3450] subsequently giving rise to excess bicarbonate. This bicarbonate may also cause the emulsification of oil in aqueous solutions after freeze/thaw degassing. [Back]
k Every coherent system is ordered, but not every ordered system is coherent. [Back]
Home | Site Index | Back: Icosahedral water clusters | Methods for investigating clusters | Brief history of water clusters | LSBU | Top
This page was established in 2000 and last updated by Martin Chaplin on 25 August, 2022