
Surface generating osmotic
pressure, repelling solutes
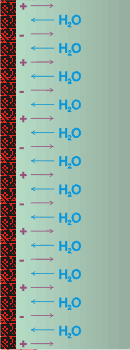
Surfaces can generate osmotic pressure without the need for solutes.
![]() The osmotic pressure of particles and membranes
The osmotic pressure of particles and membranes
![]() Exclusion zone (EZ) water
Exclusion zone (EZ) water
![]() Proposal for the generation of osmotic pressure at aqueous interfaces
Proposal for the generation of osmotic pressure at aqueous interfaces
![]() Similarities of EZ-water to osmotically-generated surface water
Similarities of EZ-water to osmotically-generated surface water
![]() Overview of conventional colligative properties
Overview of conventional colligative properties
![]() Conventional osmotic pressure
Conventional osmotic pressure
![]() Nanobubbles
Nanobubbles
![]() Osmotic pressure stabilizes nanobubbles
Osmotic pressure stabilizes nanobubbles
'The validity of a theory is not established by the number of words written
in expounding it, but by its conformity with experimental facts.'
Joel H. Hildebrand, 1979
'It is not a great sin to be wrong; it is a great sin to be boring'
Richard Saykally, 2018
Although there remains some contention amongst physical chemists over how to describe osmotic pressure, it is generally agreed that osmotic pressure is a reversible thermodynamic colligative property. It correlates well with other colligative properties such as the freezing point depression. As such, the osmotic pressure ideally depends on the number of dissolved ‘particles’ (e.g., molecules) present in a volume of liquid. It is, perhaps, unsurprising that ion exchange surfaces can generate very high osmotic pressures of over 100 MPa in water [1669], as they create high surface concentrations of counter-ions (100 MPa is the equivalent of 10 km head of water). However, the contained electrolytes in an ion-exchange resin produce a more substantial osmotic pressure than if they were free (uncontained). Thus, nanoparticles coated with immobilized polyelectrolytes can produce up to two hundred times the osmotic pressure than the same quantity of free electrolytes [2404], clearly establishing that osmotic pressure can be generated under non-colligative conditions. Poly-ionic nanoparticles, with high surface areas, produce such a substantial osmotic pressure (far more significant than expected due to counter-ions) f that they are used in practical desalination processes [1768a,d,f,h]. Likewise, polyelectrolytes may also produce high osmotic pressures between molecules (about 100 MPa) [2006]. However, hydrophilic uncharged molecules such as dextran and polyvinyl alcohol (PVA) [3277], without any counter-ions, also produce high osmotic pressures similar to polyelectrolytes [2006]. Also, it has been verified experimentally that uncharged hydrophilic particle surfaces generate high osmotic pressure without the presence of counter-ions or free solutes [1768b,c,g,h,i]. Thus, neutral uncharged triethylene glycolated particles [2404] and carbon particles coated in neutral N-isopropylacrylamide [1768g] both generate considerable osmotic pressure, if less than similarly coated poly-acrylic acid particles. Anomalously high osmotic pressures may occur within low-permeability shale [2795]. Therefore, it is clear that relatively small numbers of particles, far less than required by the ‘conventional’ colligative law, can generate high osmotic pressures so long as they possess extensive hydrophilic surfaces [1772]. This is entirely in agreement with classical (Einstein, [806]) ideas concerning osmotic pressure and its relationship to Brownian motion.
The lowered water activity within particles and membranes needs some explanation. First, the water within behaves as though it is under hydrophilic confinement, plus it will be held more strongly due to capillarity. Both these effects increase the particles and membranes grip on their water, lowering their water activity. Additionally, where polyelectrolytes are concerned, the high concentration of fixed binding sites for the counter-ions prevents their easy loss from the particles or membranes, with any counter-ion loss causing a significant energy-consuming charge separation between the enclosed solution and the bulk.
Osmotic pressure is generated within a confined volume or at a surface when insufficient water can flow onto or away from the surface. The question arises as to what happens next. Tension arises in the neighboring water, or else there will be an interface of neighboring water molecules with very different chemical potentials. Maybe this will be slightly relieved by releasing some ions, if present, but with energetically unfavorable charge separation. Alternatively, the low potential water molecules must transfer their reduced entropy to their neighbors away from the surface until balanced by the averaged energy of 'bulk' water. The reduced entropy will encourage increased organization within the surface of unstirred water. If the water inside a sunken capillary is considered, this effect will cause flow out of a capillary tube [2669], followed by a circular flow through the sunken capillary.
Microphotograph, from [1740]
![based on microphotograph from [1740] based on microphotograph from [1740]](images/ez.gif)
Much work has been done in the laboratory of Gerald Pollack concerning the non-equilibrium mesoscopic properties of aqueous solutions next to surfaces [1328, 1740, 2274, 2387, 2669]. c Earlier independent workers have reported similar results going back more than 100 years [2058, 2751, 2790]. In essence, it has been found that the interfacial water next to ionic charged surfaces (e.g., polyacrylate, see right from [1740], Nafion e, charged Pt [2792]), or neutral uncharged (e.g., polyvinyl alcohol, cellulose acetate, cellulose [2702], quartz [2715], titanium dioxide, silicon, colloidal gold, aluminum j, contact lens, muscle, rabbit cornea [2790], bacteria, and low-water content but hydrophilic fats [2876]), and hydrophilic surfaces expel positive and negative solutes to the bulk of the solution that may be several hundred microns away. These exclusion zones (named as
Microphotograph, from [1739]
With a laser tweezers system, the existence of force fields inside the solute-free EZ has been found to reduce as a function of distance from the surface [1784]. Microspheres introduced into the EZ move away from the interface to the furthest extent of the EZ, so showing the force remains even in the exclusion zone, and no new phase had formed there [2169] (which might have been expected to prevent such movement). The process is a kinetic-diffusive process, like osmosis [3261]. The particles also develop their own EZs [2704]. The movement of the EZ boundary follows a power law close to that expected for free diffusion [2169]. Also, the EZ-water has been shown to possess other physical properties such as an absorption peak at 270 nm, a higher refractive index, a greater permittivity, a greater density, a greater viscosity, and a negative charge compared with the bulk water. The 270-nm absorption has also been found unexpectedly in various aqueous solutions of low molecular weight uncolored solutes [1328a], showing it to be a property of the water rather than the solutes.
Further, it has been found that uncharged hydrophilic reverse osmosis fibrous membranes efficiently operate as osmotic membranes despite possessing larger pores than the usual molecular-sized pores. This finding shows that they must present thick multi-molecular layers of water that are relatively impenetrable to low molecular mass salts and molecules. It has also been independently experimentally verified that uncharged but highly hydrophilic nanoparticles with high surface areas produce such an enormous osmotic pressure that they can be used in practical desalination processes [1768a,b]. Also, uncharged hydrophilic polymers have been shown to generate osmotic pressures of greater than MPa at nanoscopic distances [2006]. The 1 - 3 mm thick interfacial zone of water found at quartz surfaces in 60 ˣ 20 µm2 quartz cavities has its mprominent infrared peak at 3200 cm−1 indicating more strongly linked hydrogen-bonding by about +1 kJ ˣ mol−1 throughout this zone of vicinal water [2715].
Electric fields (of about 109 V ˣ m−1), in water vapor, form one-dimensional water nanowires consisting of square or pentagonal prism-like structures along the electric field [3724]. It appears likely that such commonly-found electric fields next to water surfaces initiate such structuring and the related ES structuring. Vicinal water, extending for tens of nanometers but well within the unstirred 'Nernst' layer near inert solid surfaces, has been found to have properties consistent with the partial conversion to low-density water; for example, reduced density (-4%) and raised dielectric, specific heat (+25%), compressibility (+20 - 100%), and viscosity (+200 - 1100%) [205]. The thermodynamic rationale for forming this (interfacial) vicinal water is that the loss of hydrogen bonds at the surface increases the enthalpy necessitating the water molecules to compensate by doing pressure-volume work. The network expands to form low-density water with lower entropy (see also hydrophobic surfaces and, for example, [480]).
Contrasting these experimental studies, theoretical studies using molecular water models show no extension of the interface beyond the ultra-thin external surface [2198]. However, such studies do not explain the experimental results. For example, by measuring electrostatic forces, water shows an anomalously low dielectric constant (≈ 2) next to boron nitride (BN) surfaces. The depth of this (out-of-plane dielectric constant ≈ 2) layer is about 0.75 nm (3 water layers), it remains anomalously small (out-of-plane dielectric constant < 20) up to 20 nm and does not return to its bulk value (dielectric constant ≈ 80) for ≈ 500 nm [3373]. Interestingly, where solid surfaces interact strongly with contacting liquids (including water but not exclusively so), there are non-negligible interfacial effects. Shear flow infrared experiments can reveal these to extend up to several millimeters into the bulk [2913]. Liquid flowing slowly over the wetting surfaces produces cooling due to stretching, while frictional interactions produce heating at fast rates .
Up till 2020, there was no generally accepted explanation for these experimental phenomena or properties. However, below is a new explanation that is very simple, easily understood, and potentially very important in several related fields.
Wherever water is present in a solution, it may be considered either 'bound' or 'free' (bulk), although there will be transitional water between these states. When considering the colligative properties, 'water' is considered bound to any solute when it has a very low entropy compared with pure liquid water. Such water is considered part of the solute and not part of the dissolving 'free' (bulk) water [1064]. Pure liquid water consists of a mixture containing low-density water, extensively hydrogen-bonded structures, and higher-density water, consisting of a mixture of chains and smaller, less extensive clusters. The proportions of 'bound' or 'free' water in pure liquid water can vary; the strongly bound larger clusters behave like 'bound' water. In bulk liquid water, the relative concentrations of the two aqueous forms are of no consequence as all the water behaves the same throughout.
Affect of the surface on water activity
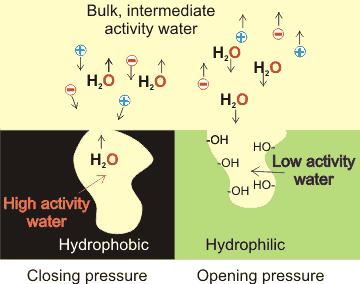
Suppose volumes of the solution contain different proportions of strongly and weakly hydrogen-bonded water molecules (or even more simply that there is more extensive clustering present). In that case, these different volumes will show a difference concerning their water activity, chemical potential, and internal pressure. h Usually, any such instantaneous differences in the water activity and chemical potential between different volumes within the same mass of a liquid would rapidly cause liquid movement from one to the other. In this manner, these different states equalize, so removing any potential differences. However, where surfaces instantaneously interact with the liquid water, the concentration of the more extensive hydrogen-bonded clusters differs from the bulk values with the surface interactions preventing the potential equalization between bulk and surface volumes [3216]. When this occurs, the surface water has a lower water activity and lower chemical potential than the bulk. This lower chemical potential eads to differences in osmotic pressure and other colligative properties such as freezing point and 'opening' pressures (see above left). In contrast, volumes of water within hydrophobic clefts and pores (see above left) have higher activity than bulk water, whereby the water tends to vacate the clefts, creating 'closing' pressures. This tendency has been shown in both hydrophobic [3130] and hydrophilic [3135] clefts. It has also been demonstrated that the water cavitation within such pores may depend on the orientation of hydrophobic groups situated on the pore's rim. These can trigger the drying of nonpolar pockets in liquid water [3993].
This behavior of water, causing the creation of dry low-dielectric nm-size environments, has been described as primary importance to living organisms, as examples, effective in DNA binding, gene recognition, and enzyme catalysis [3619]. In addition, it enables the strong recognition power of hydrogen bonding.
Self-generation of osmotic pressure at interfaces

The change in the chemical potential (Δμw) is,
Δμw = –{RTLn(xws) -RTLn(xwb)}
(that is, a negative energy term is added to the chemical potential when xws < xwb) where xws is the mole fraction (activity) of the ‘free’ water (0 < xws < 1) in the surface layer and xwb is the mole fraction (activity) of the ‘free’ (bulk) water (0 < xwb < 1) in the bulk liquid.
Small reductions in water activity give rise to large osmotic pressures
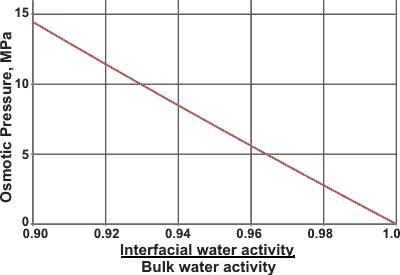
The generated osmotic pressure (Π) is given by,
![]()
where VM is the molar volume of water, and p/po is the ratio of the partial pressures of solution (p) and pure water (po) (relative humidity). Quite small reductions in the interfacial water activity give rise to considerable osmotic pressures (see right).
At hydrophilic surfaces, interactions between the surface and neighboring water molecules establish the localized hydrogen bonding. Together with steric factors, this increases the cluster extent and lifetime [2059].b As the ‘free’ water reduces compared with its bulk value when the formation of longer-lived and more extensive hydrogen-bonded clusters increases, the water activity reduces, and the osmotic pressure increases. Solutes next to the surface will move to equalize the water activity throughout the liquid. In other words, the osmotic pressure generated next to the surface will displace solutes from the surface towards the bulk until its effect compensates the osmotic pressure of the surrounding solution or the system reaches a steady state.
A typical unstirred layer
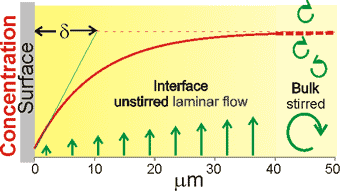
As the first effect of this solute expulsion is naturally the non-equilibrium formation of an increased concentration band as expelled solute mixes with the initial solute concentration, the extent of the expulsion will affect the whole of the unstirred layer. The effect of the surface will decay exponentially out to the stirred bulk (the Nernst layer, δ ≈ 1-100 µm or more if unstirred pure water, see diagram right) with a thickness dependent on the cube root of the diffusivity of the solutes [2699]. g The unstirred layer is not stationary but is a region of slow laminar flow parallel to the surface where transport is by diffusion rather than advection. The thickness of the layer, δ, is less than the actual thickness but rather an operational thickness (see right) defined by the equivalent uniform concentration gradient. As the diffusion of hydrogen ions is several times greater than hydroxide ions, the unstirred layer becomes negatively charged with developing charge separation. i After a considerable time (much greater than minutes), dependent on the vessel size and shape, an equilibrium water activity will extend over the entire liquid up to the surface of the solid. The liquid structuring will not be constant over this volume.
Where hydrophilic microparticles or nanoparticles are suspended in aqueous solutions, their surfaces will necessarily cause mutually repulsive, non-equilibrium, osmotic pressure effects. These that may result in the ordering of the particles for considerable periods (much greater than minutes) within small volumes of the liquid [272a, 2060].
Note that the non-equilibrium osmotic drive does not require a material membrane to separate the two solutions [1744], provided there are two distinct volumes (e.g., [1669]). Here the two phases consist of the unstirred and stirred layers. In this context [1739], the affected aqueous layer behaves similarly to that described for the exclusion zone (EZ) water by Pollack and forms a simple explanation of his experimental data [1740]. It also shows similarities with the experiments on autothixotropy [509, 1898, 1975].
Other experimental properties of the EZ layers, such as the reduction in its thickness with the particle size causing the effect [2062], and the effect of increased bulk ionic strength [1328b], are easily explained by the presented hypothesis. The unstirred layer around particles depends on the particle size and high bulk osmotic pressures and will oppose the osmotic pressure at the hydrophilic surface. An interesting alternative explanation of the EZ layers, using Nafion,e involving diffusiophoresis, has been proposed [2808] but cannot explaini most of the cases of EZ-layer formation.
A standing electromagnetic wave
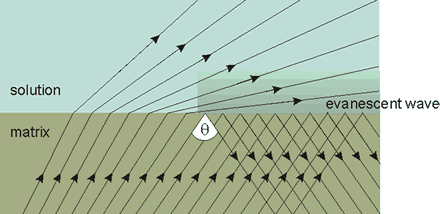
Another effect of interfaces is the formation of evanescent waves due to the internal reflection of electromagnetic radiation. The standing electromagnetic evanescent wave within the interfacial water is caused by impinging electromagnetic radiation and the angle at which total internal reflection occurs (θ). The standing electromagnetic wave interacts with water molecules to stabilize a standing wave of hydrogen-bonded clusters (coherence, lower entropy). In agreement with the experimental data [1173, 1589, 1741, 2704], this alters the local concentration and extent of hydrogen-bonded clusters so increasing the above osmotic effect. The distance range affected is governed by the wavelength (> 200 nm), whereby a coherent (or partially coherent) structure may emerge [3712]. It has also been shown that infrared radiation increases the hydrogen-bonded interactions of water molecules in protein hydration shells [2489]. Therefore, irradiation of the stretch vibration modes of the elongated water clusters increases the size of the coherent (orderly, lower entropy) regions [1691] of the water and their degree of coherence (orderliness, reduced entropy). It has been found that bulk water can be efficiently aligned by THz laser fields around 12 THz (400 cm−1), matching the single molecule's reorientational time in the bulk phase at equilibrium [3489].
It appears that a similar effect on solutes to the one described for water may occur in other polar solvents that can form hydrogen bonds [1742]; thus reinforcing the likelihood that the mechanism does not depend on any specific properties of water, such as the here-described colligative thermodynamics. Increasing ethanol to water gives a maximum exclusion zone width at about 12 % v/v followed by a decrease to about half the pure water width at 95 % v/v ethanol [3145].
Typical surface density, as described by molecular models
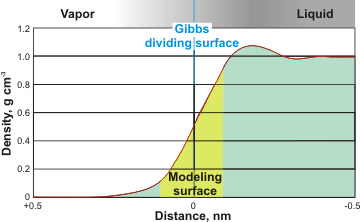
There is no a priori reason why the same phenomenon as described above should not also apply to gas/liquid interfaces. The surface of water differs from the bulk as the density decreases to zero in a complex manner. See left for the typical density at the surface, as shown by modeling studies. There is much direct evidence for an effective depth of the liquid surface of many nanometers [2751]. In addition, the presence of an extensive EZ layer (up to 4 mm at a flat surface) at the gas-liquid interface has been confirmed experimentally [2389].
The generation of the osmotic pressure at the surface is due partly to the necessarily under-coordinated water molecules at the gas-liquid interface forming an ice-like, low-density phase [2004] that has lower water activity than the bulk water, and partly to the higher solute concentration formed just under the interface. In addition, the remaining hydrogen bonding in the surface is stronger than in the bulk [1261], due to the reduced competition from neighboring water molecules, lower anti-cooperativity, and compensation for the increased chemical potential on the loss of some bonding.
There is now much evidence that sub-micron-sized gas-filled cavities (often called nanobubbles) can exist for a significant time both in bulk aqueous solution and submerged aqueous-hydrophobe interfaces. Their contained gas is in constant flux, with gas molecules both leaving and entering continuously. The cavities are under excess pressure given by the Laplace equation (2γ/r, where γ is the surface tension and r is the cavity radius). The surface tension causes a tendency to minimize their surface area and volume. Nanobubbles grow or shrink by diffusion according to external pressure and the degree of over-saturation or under-saturation in the surrounding solution, with the dissolved gas relative to the raised cavity pressure. As the solubility of gas is proportional to the gas pressure, and this pressure is exerted by the surface tension in inverse proportion to the size of the bubbles, there is an increasing tendency for gases to dissolve as the bubbles reduce in size. This accelerates the bubble-dissolution process. The bubble's movements and contractions increase such size-reduction during this activity, which aids the removal of any gas-saturated solution from around the cavities.
Present theoretical calculations show that nanobubbles should only persist for a few microseconds, in contrast to their long lifetimes (hours to days) as detected experimentally by light scattering, or resonant mass measurement (bulk nanobubbles [1972]), or tapping mode atomic force microscopy (surface nanobubbles). Interestingly, these cavities (bubbles) are subject to Brownian motion, behaving as though they have solid shells similar to solid nanoparticles. Furthermore, surface and bulk-phase nanobubbles can both give rise to the otherwise difficult to explain long-range attraction between hydrophobic surfaces due to bridging nanoscopic gas cavities or an osmotic effect due to local nanobubble depletion.
A further reason for at least some of the stability of nanobubbles is that the nanobubble gas/liquid interface is charged [1591], expanding the surface and introducing an opposing force to the surface tension, so slowing or preventing the nanobubble dissipation. It is clear that the presence of like charges at the interface will reduce the effect of the surface tension, with charge repulsion acting in the opposite direction to the surface minimization due to surface tension. Any effect may be enhanced by the presence of additional charged materials that favor the gas-liquid interface, such as OH− ions at neutral or basic pH [1591]. It has been proposed that the surface tension is reduced by the degree of supersaturation at the surface [2013]. This supersaturation is prevented from equilibrating away from the bubbles by the imposed osmotic pressure, this introduces a further stabilization effect on the nanobubbles.
The generation of osmotic pressure at nanobubble surfaces
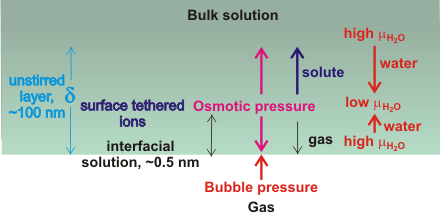
Contributing to the stability of nanobubbles is the slow rate of gas diffusion to the bulk liquid surface from both surface and bulk-phase nanobubbles [1973, 1987]. In particular, nanobubbles in a cluster of bulk nanobubbles protect each other from diffusion by a shielding effect [2074]. A thick interfacial layer, a phenomenon experimentally supported by the higher forces required to penetrate the nanobubbles' interface [1986, 1987]. Note that the interface has extensive volumes on both sides where there is laminar flow orthogonal to the surface only. Here we assume that the cause of this layer is the osmotic pressure produced by solutes [2406] and water structuring beneath the gas-liquid interface [2057]. This is also the cause of the experimentally visible EZ-water layer [2389], preventing the gas from dissolving towards the bulk and driving any dissolved gas near the interface back into the nanobubble (see above left). The depth of the ‘unstirred’ layer (δ) is approximately proportional to the size of the nanobubbles due to their Brownian motion. This thickness reduces on mixing caused by any surface changes in the bubbles as they rise or change size. A higher osmotic pressure around bubbles has been suggested to explain why bubbles fail to coalesce, although its origin was unproven [2536]. In support of this model, it has been found that ion-ion interactions at the air-water interface behave as surface tethered ions with stronger ion-pairing [3428].
'it is superfluous to suppose that what can be accounted for by a few principles has been produced by many'
Thomas Aquinas, written 1265-1274
Once the osmotic origin of the EZ water is accepted, other properties of the EZ-water are rationalized. It is interesting to hypothesize the effect of removing ions (including H3O+ and OH−) from water within the exclusion zone due to the interfacial osmotic pressure. Ions would typically terminate hydrogen-bonding 'wires' within the aqueous milieu. The absence or reduction of such terminations allows more extensive hydrogen bonding and consequent structuring of the low-density and high-density forms of water. This does not necessarily lead to a higher fraction of the low-density form, just that both such clusters will be more extensive and aligned. Such fiber-like structures have been found in EZ-water [3283]. Also, the higher activity, denser, CS water would move preferably towards the low-activity surface as it possesses the higher water activity out of the water clusters present. As such, the water will have somewhat different properties, explaining the experimentally found properties of EZ-water. Examples are the changed UV absorption that indicates altered structuring [1328a], the higher refractive index indicating higher density [2793], the higher viscosity indicating stronger hydrogen bonding, the slower diffusion indicating greater clustering [2792c], the lower spin-lattice relaxation times (T1 ) indicating slower dynamics [2792c], the increased birefringence suggesting a liquid-crystalline zone next to the surface, and the high permittivity indicating an unusual alignment of water dipoles [2792b]. As found in EZ water, the increase in density at the interface has been explained previously by the increase in clustering, causing the water to behave as though it is at a lower temperature, which also explains the ease with which this surface layer freezes. The presence of 270-nm absorption in the interfacial water, as described for EZ water [1328], has been ascribed to the delocalization of electrons within the extended clustering, particularly the presence of pentameric rings. d As the lowest unoccupied molecular-orbitals (LUMOs) of the clusters are both huge and of relatively low energy, these electron delocalizations are stabilized by adding an electron but not a proton. This causes the charge separation seen at these interfaces [1744, 2061].
In conclusion, the self-generation of colligative properties at hydrophilic interfaces is a simple explanation for the properties of the existing wide-ranging solvent interfaces. As such, it fulfills Occam's razor "Plurality is not to be posited without necessity."
'When you hear hoofbeats, think of horses not zebras'
possibly Theodore E. Woodward, 1940s
a This theory [2057] was first presented at the international conference 'Water and Nanomedicine', Academy of Sciences and Arts of Republic of Srpska, Banja Luka, Aug. 30, 2011 [1772]. [Back]
b This agrees with the earlier proposition for long-range water ordering involving the partial alignment of water molecules induced by the surface [1328]. [Back]
c Pollack's ideas and experiments have been the subject of a critical analysis giving an alternative view involving concentration gradients [2036a, see also 3800]. This, in turn, was rebutted by Pollack [2036b]. However, there does not seem to be any good reason to resuscitate the planar hexagonal water structuring hypothesis as proposed in the polywater debacle to explain EZ-water. This outlandish hypothesis is probably the reason why more mainstream scientists have largely ignored the undoubtedly genuine experimental data. [Back]
d An alternative (if scientifically unacceptable) view of the 270 nm absorption has been given in terms of an (improbable) highly charged extensive planar hexagonal ice-like model [2077]. [Back]
Partial Nafion® structure
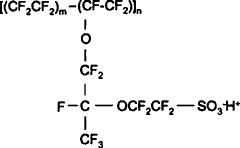
Nafion® (manufactured by DuPont) is a sulfonated tetrafluoroethylene-based fluoropolymer-copolymer [1880] that strongly absorbs water [3242]. It has excellent chemical and electrochemical stability and high proton conductivity but limited operating temperature (< ≈ 80 °C). Nafion® has hydrophilic side chains, on a hydrophobic core, organized to form a network of interconnected channels and nanometric (2–6 nm) cavities. These fill with water upon hydration and partially empty on dehydration, enabling the water transport through the membrane and supporting excellent proton conduction. Exposure of a Nafion®117 membrane to elevated temperatures and pressures (up to 150 °C and 0.7 MPa) in liquid water leads to excessive swelling, substantial changes to its internal structure, and disruption of its conductive channel network [3386]. Nafion has been extensively used in EZ (exclusion zone) experiments.
Although proposed to be stable in earlier experiments, it has been proposed to produce a slowly separating colloidal crystal at its surface [2388], produces attached outgrowths of Nafion microfibers [2388d], and release a large number of protons [2388c]. At higher temperatures, a proportion will dissolve in proportion to its swelling [3243]. If correct, this may call into question much of the EZ work using this material and confuse the fundamental properties of the EZ, mainly as Nafion has been the material of choice in many studies as it shows a maximal and easily obtained EZ. However, work on EZ using other hydrophilic materials is not affected by this finding. In 2020 it was proposed that the EZ formation is due to the unwinding of polymer fibers into the liquid bulk [4361]..
Investigations into the water content of Nafion and other sulfonated polymers showed strong relationships among the different types of water (strongly bound, weakly bound, and free) dependent on the charge density and distribution [2888]. A model of the Nafion® membrane, incorporating water content, activity-dependent diffusivity, and volume expansion have been used to resolve Nafion's water activity profiles [3205]. About 40–60% of water content remains unfrozen at −70 °C, starting from the center of the nanopores and increasing gradually as the temperature decreases [4250]. This indicates a decrease in the water activity from the pore center to the polymer surface throughout Nafion®.
The closely-related proton-exchange membranes (disulfonated poly(arylene ether) and polyimide copolymer) have been discussed [3163]. [Back]
f As the length of linear polyelectrolytes increase, the chains fold up into balls with consequent osmotic pressure increase [2705]. [Back]
g The Nernst layer. Walther Hermann Nernst, (1864 – 1941) was a German chemist who won the 1920 Nobel Prize in chemistry. The Nernst layer is a theoretical layer corresponding to the green line in the above Figure which shows the concentration profile along the direction perpendicular to a catalytic surface coinciding with the tangent to the true concentration profile at the interface. The effective thickness δ of this diffusion layer is that it would have if the concentration profile were a straight line coinciding with the tangent to the correct concentration profile at the interface. That straight line is extended up to the point where the bulk is reached.
It is impossible to stir any solution right up to an interface. There is always an unstirred layer adjacent to the surface, usually extending between 20 μ to 0.5 mm thick, even with stirring. Vigorous stirring will reduce this but still leave unstirred layers several µm thick, dependent on the diffusivity. Excessive stirring has no further effect due to the bulk turbulence as there is always laminar flow at the surface.
The Knudsen layer. The Knudsen layer is a similar non-equilibrium unstirred layer (named after Martin Knudsen, 1871 - 1949) on the gas side of the gas-liquid interface. The thickness of this layer is several times the mean free path of the mixture. The mean free path is proportional to the viscosity and the square root of the temperature, and inversely proportional to the pressure and the square root of the molecular mass of the mixture. At 20 °C and atmospheric pressure, the mean-free path of water vapor and dry air are 2.16 µm and 0.07 µm. [2714]. [Back]
h The pressure (P) exerted outwards by the liquid is given by [3262]:
![]()
where V is the volume, U is the internal energy (the sum of the kinetic energy and the intermolecular potential energy of the particles; U = Ukinetic + Upotential ), and T is the temperature. The first term on the right-hand side is the so-called “thermal pressure”, and the second term is the so-called “internal pressure”. The thermal pressure may be interpreted as the pressure arising from the thermal energy of the molecules (kinetic energy)
Noting that
![]() and
and ![]()
where a is the thermal expansion coefficient, and b is the isothermal compressibility of the liquid phase.
Then as,
![]()
![]()
Generally, the Tα/β term is much larger than an ambient pressure term the internal pressure is given by
![]()
However, for water, this term is sensitive to temperature, being -421 MPa at -30 °C, zero at 4 °C and +205 MPa at +30 °C. This is due to its heavy dependence on the relative concentrations of low-density water to high-density water.
[Back]
i It is expected that the remaining unstirred water is still dissociating but at a reduced rate due to the more extensive hydrogen bonding. This would give rise to a small electric current within the EZ-water. The pH within the EZ-water remains undetermined. [Back]
i Repetition of this work did not find an exclusion zone [3414]. [Back]
Home | Site Index | Conventional colligative properties | Water activity | The anomalies of water | Water: Introduction | The icosahedral water clusters | LSBU | Top
This page was established in 2014 and last updated by Martin Chaplin on 14 March, 2022