
![]() The heat of fusion of water with temperature
exhibits a maximum at -17 °C
The heat of fusion of water with temperature
exhibits a maximum at -17 °C
![]() Water has over twice the specific
heat capacity of ice or steam
Water has over twice the specific
heat capacity of ice or steam
![]() The specific heat capacity (CP and CV) is unusually
high
The specific heat capacity (CP and CV) is unusually
high
![]() The specific heat capacity CP has a minimum at 36°
The specific heat capacity CP has a minimum at 36°
![]() The specific
heat capacity (CP) has a maximum at about -45 °C
The specific
heat capacity (CP) has a maximum at about -45 °C
![]() The specific
heat capacity (CP) has a minimum with respect to pressure
The specific
heat capacity (CP) has a minimum with respect to pressure
![]() The heat capacity (CV) has a maximum
The heat capacity (CV) has a maximum
![]() The high heat
of vaporization
The high heat
of vaporization
![]() The high heat of sublimation
The high heat of sublimation
![]() The high entropy
of vaporization
The high entropy
of vaporization
![]() The thermal conductivity of water is
high and rises to a maximum at about 130 °C
The thermal conductivity of water is
high and rises to a maximum at about 130 °C
Enthalpy of fusion of hexagonal ice at 101,325 Pa,
from [15 ]
![Enthalpy of fusion of hexagonal ice at 101325 Pa; [15] Enthalpy of fusion of hexagonal ice at 101325 Pa; [15]](images/enthapy_of_fusion.gif)
The change in the heat of fusion of
water with temperature has a maximum at -17 °C. This strange behavior [15 ] (see right) has been determined from the variation
in the specific heat capacities (Cp) of ice and water. It is
due to changes in the structuring of supercooled water. As the temperature
is lowered from 0 °C, the hydrogen-bond strength of ice increases
due to the reduction in their vibrational energy, which gives
rise to an increasing difference (as the temperature is lowered) between
the enthalpies of the water and ice. At low temperatures (below about
-17 °C), the continued shift, with lowering the temperature, in the
supercooled water
CS![]() ES equilibrium towards the ES structure reduces the enthalpy of the liquid water relative to the
ice due to the consequent increase in hydrogen-bond strength, and
this causes the drop in the heat of fusion with lowering the temperature.
ES equilibrium towards the ES structure reduces the enthalpy of the liquid water relative to the
ice due to the consequent increase in hydrogen-bond strength, and
this causes the drop in the heat of fusion with lowering the temperature.
The enthalpy of fusion of hexagonal ice (6.007 kJ ˣ mol−1) is only a fraction of its heat of sublimation (51.059 kJ ˣ mol−1) at 0 °C. From this, only 11.8 % of the bond strength is lost during the melting process. This coincides with a 9.1 % increase in density.
[ ![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
Water has the highest specific heat of all liquids except
ammonia. The values for CV and CP are 4.1375 J ˣ g−1 ˣ K−1 and 4.1819 J ˣ g−1 ˣ K−1at 25 °C, respectively (compare CP pentane 1.66 J ˣ g−1 ˣ K−1). The large heat capacity causes water to absorb and release heat at much slower rates than similar materials. As water is heated, the increased movement of water
causes the hydrogen bonds to bend and break. As the energy
absorbed in these processes is not available to increase the
kinetic energy of the water, it takes considerable heat to
raise the water's temperature. Additionally, as water is a light molecule,
more molecules per gram than most similar molecules
absorb this energy. Heat absorbed is given out on cooling,
so allowing water to act as a heat reservoir for the Earth's surface, buffering against
temperature changes. Thus, the water in our oceans stores vast amounts of energy, so moderating Earth's climate.
Also, the high water content within our bodies (99% of the molecules present) allows us to control our body temperature more efficiently. [ ![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
Specific heats of ice, liquid water, and steam,
from [4227]
![Specific heats of ice, liquid water and steam, from [4227] Specific heats of ice, liquid water and steam, from [4227]](images/ct.gif)
At its melting point, the CP of ice-Ih and water are 37.77 J ˣ mol−1 ˣ K−1 and 76.01 J ˣ mol−1 ˣ K−1, respectively (the specific heat of liquid water being 2.01x that of ice at the melting point, see right [4227]). At its boiling point, the CPs of steam and water are 37.47 J ˣ mol−1 ˣ K−1 and 76.014 J ˣ mol−1 ˣ K−1, respectively (the specific heat of water being 2.03x that of ice at the boiling point). Interestingly, the specific heat of liquid water throughout its range is about 9 ˣ R = 74.8 J ˣ mol−1 ˣ K−1, being 1.006 ˣ 9 ˣ R at its temperature minimum. The specific heats of ice at the melting point and steam at the boiling point are 1.009 ˣ 9/2 ˣ R and 1.001 ˣ 9/2 ˣ R, respectively. This behavior has been described as consistent with a tetrahedral arrangement of liquid water molecules [3105]. The anomalous behavior of water may be compared with that of benzene, where
CP liquid = 1.03 ˣ CP solid.
The CP's of the other ices may be up to about 40% higher
( ice-three) than that of ice-1h but are
all significantly lower than liquid water [606].
The specific heats of polar molecules do increase considerably on
melting, but water shows a particularly large increase [1723]. As water
is heated, much of the energy is used to bend the hydrogen bonds;
a factor not available in the solid or gaseous phase. This extra
energy causes the specific heat to be greater in liquid water. The
presence of this large specific heat offers strong support for the
extensive nature of the hydrogen-bonded network of liquid water.
[![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
It is usual for the isobaric specific heats (CP) of liquids to increase with increased temperature at all temperatures. However, in water, the isobaric specific heat also increases with decreased temperature below 36 °C and down to -29 °C [3984 ]. Rowland first discovered this anomaly in 1879.a
![]()
where CP, P, T, and S are the specific heat, pressure, temperature, and entrop,y respectively.
Also, CP is an indication of growing fluctuations of entropy, ΔS,
where kB is the Boltzmann's constant and <(ΔS)2>TP indicates the mean squared variations in entropy at constant temperature and pressure.
Variation of Cp and Cv with temperature at 100 kPa
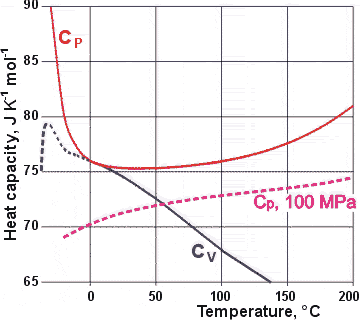
The CV values for supercooled water may be erroneous, being calculated from other data and showing an apparent discontinuity at about -20 °C. An alternative extrapolation is available [1794].
The (isobaric; also called isopiestic) specific heat capacity (CP) has a shallow minimum at about 36 °C at 100 kPa (D2O ≈ 120 °C) with a particularly steep negative slope below 0 °C [15, 67] (see right). It is interesting that this minimum is close to the body temperature of warm-blooded animals. The water cluster equilibrium shifts towards less structure (for example, CS) and higher enthalpy as the temperature is raised.
The extra positive ΔH
due to the shift in equilibrium (at low temperatures)
as the temperature is raised causes a higher CP than otherwise, particularly at supercooling temperatures
where a much more significant shift occurs [1353]. Note that generally, thermal fluctuations (<(ΔS)2>TP) increase with increasing temperature, whereas the reverse is true of supercooled water. This addition to the
CP, as the temperature is lowered, is greater
than the 'natural' fall expected, so causing a minimum
to be created. Note that CV equals CP at the temperature of maximum density. Usually, in liquids,
CP is more than 20% greater than CV.
Heat capacity at 400 MPa, from [2929]
![heat capacity at 400 MPa, from [2929] heat capacity at 400 MPa, from [2929]](images/cpp.gif)
Modeling studies using TIP4P/2005 have shown that this minimum goes to higher temperatures at higher pressure [2668 ].
As expected, the substantial specific heat changes with low temperatures are reduced at higher pressures. This specific heat-pressure minimum shifts to lower temperatures and disappears at high pressures (> 100 MPa, see above). The minimum in CP has been associated with a discontinuity in the Raman depolarization ratio (that is, perpendicular/parallel polarization) data of degassed ultrapure water and hence a weak liquid-liquid phase transition at 34.6 °C (5.8 kPa) [1044].
A further anomaly is found at higher pressure (see left), where two maxima are found at 400 MPa [2929 ]. The anomaly at this pressure is due to the interpenetration of water clustering (see elsewhere).
[![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
Heat capacity changes for liquid water and hexagonal ice
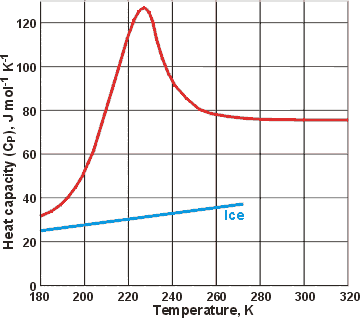
There are sizeable specific heat changes with temperature at low temperatures, but deeply supercooled water has lower specific heat at very low temperatures.There must be a maximum in the specific heat (CP)-temperature relationship at sufficiently low temperature, so long as no phase change occurs. This maximum is thought to occur where the amounts of expanded (low-density) and collapsed (higher density) structures are equal. Thus the most energy is required for their interconversion (using the icosahedral clustering model, this would be where there is 80% ES, as ES necessarily has a collapsed exterior surface). The locus of the specific heat maximum with increasing pressure (called the 'Widom' line) requires lowered temperature [1373]. At ambient pressure, the maximum is expected to lie just below the minimum temperature accessible on supercooling (232 K, [215]), although a modeling approach using TIP5P gives ≈ 250 K [1352]. The data opposite for supercooled water (upper red line) is taken from [906 ]. In 2020, temperatures down to ∼228 K were reached using evaporative cooling of ∼15-μm diameter water droplets in a vacuum. There was a sharp increase in CP from 88 J ˣ mol−1 ˣ K−1 at 244 K to about 218 J ˣ mol−1 ˣ K−1 at 229 K, where a maximum was seen [4281]. This is consistent with the liquid-liquid critical point model and explains the steep decrease in the estimated self-diffusion coefficient below 235 K. Modeling studies using TIP4P/2005 have shown that this maximum goes to lower temperatures at higher pressures and increases to higher temperatures under negative pressure [2668 ].
[ ![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
Please note that this anomaly is in doubt until the data is confirmed.
There is a minimum in the heat capacity (CP)
of liquid water with respect to pressure; ≈ 400 MPa at 290 K [606].
This may be explained as due to the break-up of the hydrogen
bonding as the pressure increases up to about 200 MPa followed by its partial
build-up, due to interpenetrating hydrogen-bonded networks,
at the higher pressures above about 200 MPa.
[![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
The CV (the heat capacity
at constant volume, CV = (δU/δT)V) of liquid water gives a maximum
in the supercooled region (shown in the calculated
values graphed above). The increase in CV in
the supercooled region is because most of the anomalous enthalpy
change is associated with the anomalous volume change. The
decrease in CV in the more deeply supercooled region is reported
as due to the decrease in van der Waals non-bonded dispersion interactions caused by water's low density [682 ]. It is evident in the calculation (using ![]() where T = temperature (K), V = molar volume (m3 ˣ mol−1), α = thermal expansivity (K−1)
and β T= isothermal compressibility
(Pa−1) as due to the great increase in the values of the thermal expansivity at low temperatures, see table [2089]).
[
where T = temperature (K), V = molar volume (m3 ˣ mol−1), α = thermal expansivity (K−1)
and β T= isothermal compressibility
(Pa−1) as due to the great increase in the values of the thermal expansivity at low temperatures, see table [2089]).
[ ![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
Comparison of the molar enthalpy of evaporation
at boiling points with related structures
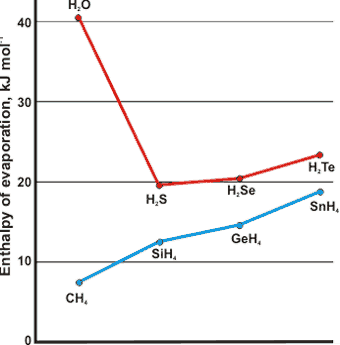
Water has the highest heat of vaporization per gram of any molecular liquid (2257 J ˣ g-1 at boiling point) and hence very low volatility but high cohesive energy density (˜ 5 ? CH4, ˜ 4 ? H2S). There is still considerable hydrogen bonding (˜ 75%) in water at 100 °C. As effectively all these bonds need to be broken (very few indeed remaining in the gas phase), there is a great deal of energy required to convert the water to gas, where the water molecules are effectively separated. The increased hydrogen bonding at lower temperatures causes higher heats of vaporization (for example, 44.8 kJ ? mol-1, at 0 °C).
Enthalpies of evaporation and fusion of molecules isoelectronic to water
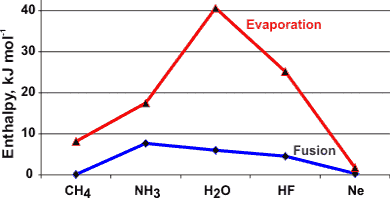
Variation of the enthalpy of evaporation with temperature
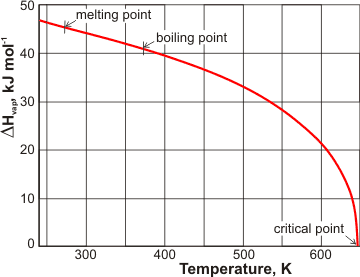
The heat of vaporization reduces to zero at the critical point (see left, [906, 1458]).
The high heat of vaporization also causes water to have an anomalously low ebullioscopic constant (that is, the effect of solute on boiling point elevation, 0.51 K ˣ kg ˣ mol−1; compare CCl4 4.95 K ˣ kg ˣ mol−1). Also related is the anomalously low cryoscopic constant of water. The high heat of vaporization allows fine water mists to be used in fighting fires by cooling flames [2456].
Surprisingly, there is a 5–10 % increase in the heat of vaporization with exposure to a high-frequency electromagnetic field (60 - 170 MHz [3788].
The high heats of fusion (6.00678 kJ ˣ mol−1 (0 °C, 101.325 kPa) [1385] ) and vaporization (45.051 kJ ˣ mol−1 (0 °C) [906 ]) combine to give rise to an anomalously high heat of sublimation (51.059 kJ ˣ mol−1at 0 °C). The heat of fusion is equivalent to the breakage of about 12 % of the hydrogen bonds. The heat of vaporization is equivalent to 100% of the hydrogen bonds remaining. From these values, the hydrogen bond strength in ice at 0 °C must equal about 25 kJ ˣ mol−1.
Water also has an anomalously high entropy of vaporization due to the hydrogen-bonded order lost on vaporization in addition to the order lost by being a liquid changing into a gas. As the heat of vaporization is also anomalously high, the ratio (ΔHvap/ΔSvap) is not anomalous.
Interestingly, the entropy of vaporization is inversely related
to the absolute temperature from the temperature of supercooled water to above
400 K (that is, ΔSvap ![]() 1/T).
[
1/T).
[![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
The thermal conductivity of water,
the supercooled data is from [1983]
![The thermal conductivity of water, the supercooled data is from [1983] The thermal conductivity of water, the supercooled data is from [1983]](images/thermal_conductivity.gif)
The thermal conductivity is shown along the saturation line (liquid-vapor equilibrium line). Note that the pressure increases with the temperature, see, phase diagram. The thermal conductivity becomes infinite at the critical point [IAPWS ].
Apart from liquid metals, water has the highest thermal conductivity of any liquid. For most liquids, the thermal conductivity (the rate at which energy is transferred down a temperature gradient) falls with increasing temperature, which occurs only above about 130 °C in liquid water [188, 4474]. A similar difference is noted for the thermal diffusivity [4474] (thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure, m2 ˣ s −1, measuring the rate of transfer of heat (temperature) of a material from the hot end to the cold end).
Additionally, If carefully drawn using the original data (rather than a smoothed curve), there appears to be a kink at about 64 °C [2755, 2756].
As water's temperature is lowered, the rate at which
energy is transferred is reduced to an ever-increasing
extent. Instead of the energy being transferred between
molecules, it is stored in the hydrogen-bonding fluctuations
within the increasingly large clusters at lower
temperatures. When the thermal energy increases, it shifts the e ES![]() CS equilibrium towards the CS structure, which possesses greater flexibility and has more bent hydrogen bonds than the transference of kinetic energy.
CS equilibrium towards the CS structure, which possesses greater flexibility and has more bent hydrogen bonds than the transference of kinetic energy.
If our cells produce excess energy, that heat energy is transported away more efficiently at higher temperatures, reducing its heating effect. At lower temperatures, with lower thermal conductivity, the heat is less well transported away, allowing greater heating effect. Thus our cells are more able to stabilize their temperature.
There is a minimum in the thermal conductivity-temperature behavior just below -37 °C as the amount of fully expanded network increases and is in line with that indicated by the much higher value found for ice Ih. At lower temperatures, transformation into LDA results in a steeply climbing curve (1.4 W ˣ K−1 ˣ m−1 at 100 K) [1202]. Different modeling approaches give a thermal conductivity minimum at ≈ 255 K [1352] or ≈ 230 K [1983].
If the density is kept constant, the thermal conductivity
is proportional to the square root of the absolute temperature,
between 100 °C and 400 °C [614].
[![]() Anomalies page: Back to Top
Anomalies page: Back to Top ![]() ]
]
a H. A. Rowland, On the mechanical equivalent of heat and subsidiary remarks on the variation of the mercury from the air thermometer and on the variation of the specific heat of water, Proceedings of the American Academy of Arts and Sciences, 7 (1880) 75-200. [Back]
![]() Phase anomalies (P1-P13) explanations
Phase anomalies (P1-P13) explanations
![]() Density anomalies (D1-D22) explanations
Density anomalies (D1-D22) explanations
![]() Material anomalies(M1-M16) explanations
Material anomalies(M1-M16) explanations
![]() Physical anomalies (F1-F10) explanations
Physical anomalies (F1-F10) explanations
Home | Site Index | The anomalies of water | Water: Introduction | The icosahedral water clusters | LSBU | Top
This page was established in 2006 and last updated by Martin Chaplin on 27 July, 2022